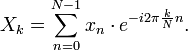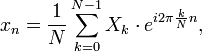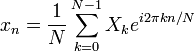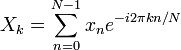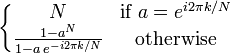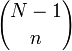Discrete Fourier transform

From Wikipedia, the free encyclopedia

Discrete Fourier transform

In mathematics, the discrete Fourier transform (DFT) is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function (which is often a function in the time domain). The DFT requires an input function that is discrete. Such inputs are often created by sampling a continuous function, such as a person's voice. The discrete input function must also have a limited (finite) duration, such as one period of a periodic sequence or a windowed segment of a longer sequence. Unlike the discrete-time Fourier transform (DTFT), the DFT only evaluates enough frequency components to reconstruct the finite segment that was analyzed. The inverse DFT cannot reproduce the entire time domain, unless the input happens to be periodic. Therefore it is often said that the DFT is a transform for Fourier analysis of finite-domain discrete-time functions.

The input to the DFT is a finite sequence of real or complex numbers (with more abstract generalizations discussed below), making the DFT ideal for processing information stored in computers. In particular, the DFT is widely employed in signal processing and related fields to analyze the frequencies contained in a sampled signal, to solve partial differential equations, and to perform other operations such as convolutions or multiplying large integers. A key enabling factor for these applications is the fact that the DFT can be computed efficiently in practice using a fast Fourier transform (FFT) algorithm.

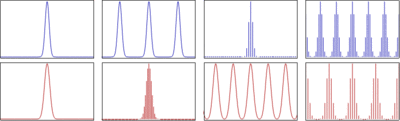
Relationship between the (continuous) Fourier transform and the discrete Fourier transform. Left column: A continuous function (top) and its Fourier transform (bottom). Center-left column: Periodic summation of the original function (top). Fourier transform (bottom) is zero except at discrete points. The inverse transform is a sum of sinusoids called Fourier series. Center-right column: Original function is discretized (multiplied by a Dirac comb) (top). Its Fourier transform (bottom) is a periodic summation (DTFT) of the original transform. Right column:The DFT (bottom) computes discrete samples of the continuous DTFT. The inverse DFT (top) is a periodic summation of the original samples. The FFT algorithm computes one cycle of the DFT and its inverse is one cycle of the DFT inverse.

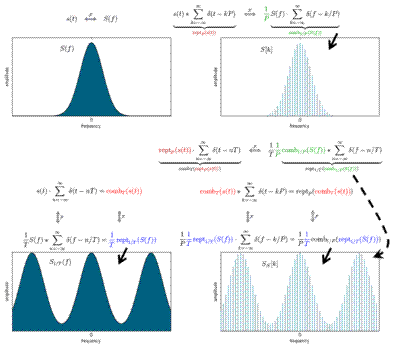
Illustration of using Dirac comb functions and the convolution theorem to model the effects of sampling and/or periodic summation. The graphs on the right side depict the (finite) coefficients that modulate the infinite amplitudes of a comb function whose teeth are spaced at the reciprocal of the time-domain periodicity. The coefficients in the upper figure are computed by the Fourier series integral. The DFT computes the coefficients in the lower figure. Its similarities to the original transform, S(f), and its relative computational ease are often the motivation for computing a DFT. The lower left graph represents a discrete-time Fourier transform (DTFT).

FFT algorithms are so commonly employed to compute DFTs that the term "FFT" is often used to mean "DFT" in colloquial settings. Formally, there is a clear distinction: "DFT" refers to a mathematical transformation or function, regardless of how it is computed, whereas "FFT" refers to a specific family of algorithms for computing DFTs. The terminology is further blurred by the (now rare) synonym finite Fourier transform for the DFT, which apparently predates the term "fast Fourier transform" (Cooley et al., 1969) but has the same initialism.

[hide]

o 2.3 The Plancherel theorem and Parseval's theorem

o 2.4 Periodicity

o 2.5 The shift theorem

o 2.6 Circular convolution theorem and cross-correlation theorem

o 2.7 Convolution theorem duality

o 2.8 Trigonometric interpolation polynomial

o 2.9 The unitary DFT

o 2.10 Expressing the inverse DFT in terms of the DFT

o 2.11 Eigenvalues and eigenvectors

o 2.12 Uncertainty principle

o 2.13 The real-input DFT

· 3 Generalized DFT (shifted and non-linear phase)

· 4 Multidimensional DFT

o 4.1 The real-input multidimensional DFT

· 5 Applications

o 5.1 Spectral analysis

o 5.2 Data compression

o 5.3 Partial differential equations

o 5.4 Polynomial multiplication

§ 5.4.1 Multiplication of large integers

· 6 Some discrete Fourier transform pairs

· 7 Generalizations

o 7.1 Representation theory

o 7.2 Other fields

o 7.3 Other finite groups

· 8 Alternatives

· 9 See also

· 10 Notes

· 11 Citations

· 12 References

· 13 External links

[edit]Definition

The sequence of N complex numbers x₀, ..., x_N₋₁ is transformed into another sequence of N complex numbers according to the DFT formula:

$X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i 2 \pi \frac{k}{N} n}.$

(Eq.1)

The transform is sometimes denoted by the symbol $\mathcal{F}$ , as in $\mathbf{X} = \mathcal{F} \left \{ \mathbf{x} \right \}$ or $\mathcal{F} \left ( \mathbf{x} \right )$ or $\mathcal{F} \mathbf{x}.$ ^{[note 1]}

Eq.1 can be interpreted or derived in various ways, for example:

§ It completely describes the discrete-time Fourier transform (DTFT) of an N-periodic sequence, which comprises only discrete frequency components. (Discrete-time Fourier transform#Periodic data)

§ It can also provide uniformly spaced samples of the continuous DTFT of a finite length sequence. (Sampling the DTFT)

§ It is the discrete analogy of the formula for the coefficients of a Fourier series:

$x_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k \cdot e^{i 2 \pi \frac{k}{N} n},$

(Eq.2)

which is the inverse DFT (IDFT). Each $X_k$ is a complex number that encodes both amplitude and phase of a sinusoidal component of function $x_n$ .

The sinusoid's frequency is $\scriptstyle \frac{k}{N}$ cycles per sample. Its amplitude and phase are:

$|X_k|/N = \sqrt{\operatorname{Re}(X_k)^2 + \operatorname{Im}(X_k)^2}/N$

$\arg(X_k) = \operatorname{atan2}\big( \operatorname{Im}(X_k), \operatorname{Re}(X_k) \big),$

where atan2 is the two-argument form of the arctan function. The normalization factor multiplying the DFT and IDFT (here 1 and 1/N) and the signs of the exponents are merelyconventions, and differ in some treatments. The only requirements of these conventions are that the DFT and IDFT have opposite-sign exponents and that the product of their normalization factors be 1/N. A normalization of $\scriptstyle \sqrt{1/N}$ for both the DFT and IDFT makes the transforms unitary, which has some theoretical advantages. But it is often more practical in numerical computation to perform the scaling all at once as above (and a unit scaling can be convenient in other ways).

(The convention of a negative sign in the exponent is often convenient because it means that $X_k$ is the amplitude of a "positive frequency", $\scriptstyle +\frac{k}{N}$ . Equivalently, the DFT is often thought of as a matched filter: when looking for a frequency of +1, one correlates the incoming signal with a frequency of −1.)

In the following discussion the terms "sequence" and "vector" will be considered interchangeable.

[edit]Properties

[edit]Completeness

The discrete Fourier transform is an invertible, linear transformation

$\mathcal{F}\colon\mathbb{C}^N \to \mathbb{C}^N$

with C denoting the set of complex numbers. In other words, for any N > 0, an N-dimensional complex vector has a DFT and an IDFT which are in turn N-dimensional complex vectors.

[edit]Orthogonality

The vectors $u_k=\left[ e^{ \frac{2\pi i}{N} kn} \;|\; n=0,1,\ldots,N-1 \right]^T$ form an orthogonal basis over the set of N-dimensional complex vectors:

$u^T_k u_{k'}^* = \sum_{n=0}^{N-1} \left(e^{ \frac{2\pi i}{N} kn}\right) \left(e^{\frac{2\pi i}{N} (-k')n}\right) = \sum_{n=0}^{N-1} e^{ \frac{2\pi i}{N} (k-k') n} = N~\delta_{kk'}$

where $~\delta_{kk'}$ is the Kronecker delta. (In the last step, the summation is trivial if $k=k'$ , where it is 1+1+⋅⋅⋅=N, and otherwise is a geometric series that can be explicitly summed to obtain zero.) This orthogonality condition can be used to derive the formula for the IDFT from the definition of the DFT, and is equivalent to the unitarity property below.

[edit]The Plancherel theorem and Parseval's theorem

If X_k and Y_k are the DFTs of x_n and y_n respectively then the Plancherel theorem states:

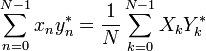
$\sum_{n=0}^{N-1} x_n y^*_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k Y^*_k$

where the star denotes complex conjugation. Parseval's theorem is a special case of the Plancherel theorem and states:

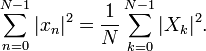
$\sum_{n=0}^{N-1} |x_n|^2 = \frac{1}{N} \sum_{k=0}^{N-1} |X_k|^2.$

These theorems are also equivalent to the unitary condition below.

[edit]Periodicity

If the expression that defines the DFT is evaluated for all integers k instead of just for $k = 0, \dots, N-1$ , then the resulting infinite sequence is a periodic extension of the DFT, periodic with period N.

The periodicity can be shown directly from the definition:

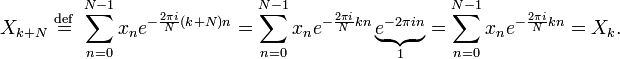
$X_{k+N} \ \stackrel{\mathrm{def}}{=} \ \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} (k+N) n} = \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} k n} \underbrace{e^{-2 \pi i n}}_{1} = \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} k n} = X_k.$

Similarly, it can be shown that the IDFT formula leads to a periodic extension.

[edit]The shift theorem

Multiplying $x_n$ by a linear phase $e^{\frac{2\pi i}{N}n m}$ for some integer m corresponds to a circular shift of the output $X_k$ : $X_k$ is replaced by $X_{k-m}$ , where the subscript is interpretedmodulo N (i.e., periodically). Similarly, a circular shift of the input $x_n$ corresponds to multiplying the output $X_k$ by a linear phase. Mathematically, if $\{x_n\}$ represents the vectorx then

if $\mathcal{F}(\{x_n\})_k=X_k$

then $\mathcal{F}(\{ x_n\cdot e^{\frac{2\pi i}{N}n m} \})_k=X_{k-m}$

and $\mathcal{F}(\{x_{n-m}\})_k=X_k\cdot e^{-\frac{2\pi i}{N}k m}$

[edit]Circular convolution theorem and cross-correlation theorem

The convolution theorem for the discrete-time Fourier transform indicates that a convolution of two infinite sequences can be obtained as the inverse transform of the product of the individual transforms. An important simplification occurs when the sequences are of finite length, N. In terms of the DFT and inverse DFT, it can be written as follows:

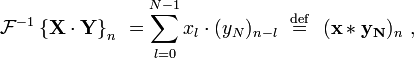
$\mathcal{F}^{-1} \left \{ \mathbf{X\cdot Y} \right \}_n \ = \sum_{l=0}^{N-1}x_l \cdot (y_N)_{n-l} \ \ \stackrel{\mathrm{def}}{=} \ \ (\mathbf{x * y_N})_n\ ,$

which is the convolution of the $\mathbf{x}$ sequence with a $\mathbf{y}$ sequence extended by periodic summation:

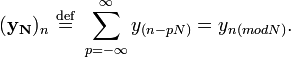
$(\mathbf{y_N})_n \ \stackrel{\mathrm{def}}{=} \ \sum_{p=-\infty}^{\infty} y_{(n-pN)} = y_{n (mod N)}. \,$

Similarly, the cross-correlation of $\mathbf{x}$ and $\mathbf{y_N}$ is given by:

$\mathcal{F}^{-1} \left \{ \mathbf{X^* \cdot Y} \right \}_n = \sum_{l=0}^{N-1}x_l^* \cdot (y_N)_{n+l} \ \ \stackrel{\mathrm{def}}{=} \ \ (\mathbf{x \star y_N})_n\ .$

A direct evaluation of either summation (above) requires $\scriptstyle O(N^2)$ operations for an output sequence of length N. An indirect method, using transforms, can take advantage of the $\scriptstyle O(N\log N)$ efficiency of the fast Fourier transform (FFT) to achieve much better performance. Furthermore, convolutions can be used to efficiently compute DFTs via Rader's FFT algorithm and Bluestein's FFT algorithm.

Methods have also been developed to use circular convolution as part of an efficient process that achieves normal (non-circular) convolution with an $\mathbf{x}$ or $\mathbf{y}$ sequence potentially much longer than the practical transform size (N). Two such methods are called overlap-save and overlap-add.^[1]

[edit]Convolution theorem duality

It can also be shown that:

$\mathcal{F} \left \{ \mathbf{x\cdot y} \right \}_k \ \stackrel{\mathrm{def}}{=} \sum_{n=0}^{N-1} x_n \cdot y_n \cdot e^{-\frac{2\pi i}{N} k n}$

$=\frac{1}{N} (\mathbf{X * Y_N})_k, \,$ which is the circular convolution of $\mathbf{X}$ and $\mathbf{Y}$ .

[edit]Trigonometric interpolation polynomial

The trigonometric interpolation polynomial

$p(t) = \frac{1}{N} \left[ X_0 + X_1 e^{2\pi it} + \cdots + X_{N/2-1} e^{(N/2-1)2\pi it} + X_{N/2} \cos(Nt/2) + X_{N/2+1} e^{(-N/2+1)2\pi it} + \cdots + X_{N-1} e^{-2\pi it} \right]$ for N even ,

$p(t) = \frac{1}{N} \left[ X_0 + X_1 e^{2\pi it} + \cdots + X_{\lfloor N/2 \rfloor} e^{\lfloor N/2 \rfloor 2\pi it} + X_{\lfloor N/2 \rfloor+1} e^{-\lfloor N/2 \rfloor 2\pi it} + \cdots + X_{N-1} e^{-2\pi it} \right]$ for N odd,

where the coefficients X_k are given by the DFT of x_n above, satisfies the interpolation property $p(2\pi n/N) = x_n$ for $n=0,\ldots,N-1$ .

For even N, notice that the Nyquist component $\frac{X_{N/2}}{N} \cos(Nt/2)$ is handled specially.

This interpolation is not unique: aliasing implies that one could add N to any of the complex-sinusoid frequencies (e.g. changing $e^{-it}$ to $e^{i(N-1)t}$ ) without changing the interpolation property, but giving different values in between the $x_n$ points. The choice above, however, is typical because it has two useful properties. First, it consists of sinusoids whose frequencies have the smallest possible magnitudes: the interpolation is bandlimited. Second, if the $x_n$ are real numbers, then $p(t)$ is real as well.

In contrast, the most obvious trigonometric interpolation polynomial is the one in which the frequencies range from 0 to $N-1$ (instead of roughly $-N/2$ to $+N/2$ as above), similar to the inverse DFT formula. This interpolation does not minimize the slope, and is not generally real-valued for real $x_n$ ; its use is a common mistake.

[edit]The unitary DFT

Another way of looking at the DFT is to note that in the above discussion, the DFT can be expressed as a Vandermonde matrix:

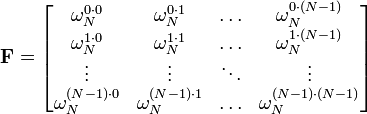
$\mathbf{F} = \begin{bmatrix} \omega_N^{0 \cdot 0} & \omega_N^{0 \cdot 1} & \ldots & \omega_N^{0 \cdot (N-1)} \\ \omega_N^{1 \cdot 0} & \omega_N^{1 \cdot 1} & \ldots & \omega_N^{1 \cdot (N-1)} \\ \vdots & \vdots & \ddots & \vdots \\ \omega_N^{(N-1) \cdot 0} & \omega_N^{(N-1) \cdot 1} & \ldots & \omega_N^{(N-1) \cdot (N-1)} \\ \end{bmatrix}$

where

$\omega_N = e^{-2 \pi i/N}\,$

is a primitive Nth root of unity. The inverse transform is then given by the inverse of the above matrix:

$\mathbf{F}^{-1}=\frac{1}{N}\mathbf{F}^*$

With unitary normalization constants $1/\sqrt{N}$ , the DFT becomes a unitary transformation, defined by a unitary matrix:

$\mathbf{U}=\mathbf{F}/\sqrt{N}$

$\mathbf{U}^{-1}=\mathbf{U}^*$

$|\det(\mathbf{U})|=1$

where det() is the determinant function. The determinant is the product of the eigenvalues, which are always $\pm 1$ or $\pm i$ as described below. In a real vector space, a unitary transformation can be thought of as simply a rigid rotation of the coordinate system, and all of the properties of a rigid rotation can be found in the unitary DFT.

The orthogonality of the DFT is now expressed as an orthonormality condition (which arises in many areas of mathematics as described in root of unity):

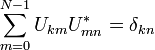
$\sum_{m=0}^{N-1}U_{km}U_{mn}^*=\delta_{kn}$

If $\mathbf{X}$ is defined as the unitary DFT of the vector $\mathbf{x}$ then

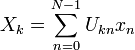
$X_k=\sum_{n=0}^{N-1} U_{kn}x_n$

and the Plancherel theorem is expressed as:

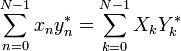
$\sum_{n=0}^{N-1}x_n y_n^* = \sum_{k=0}^{N-1}X_k Y_k^*$

If we view the DFT as just a coordinate transformation which simply specifies the components of a vector in a new coordinate system, then the above is just the statement that the dot product of two vectors is preserved under a unitary DFT transformation. For the special case $\mathbf{x} = \mathbf{y}$ , this implies that the length of a vector is preserved as well—this is justParseval's theorem:

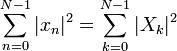
$\sum_{n=0}^{N-1}|x_n|^2 = \sum_{k=0}^{N-1}|X_k|^2$

[edit]Expressing the inverse DFT in terms of the DFT

A useful property of the DFT is that the inverse DFT can be easily expressed in terms of the (forward) DFT, via several well-known "tricks". (For example, in computations, it is often convenient to only implement a fast Fourier transform corresponding to one transform direction and then to get the other transform direction from the first.)

First, we can compute the inverse DFT by reversing the inputs:

$\mathcal{F}^{-1}(\{x_n\}) = \mathcal{F}(\{x_{N - n}\}) / N$

(As usual, the subscripts are interpreted modulo N; thus, for $n=0$ , we have $x_{N-0}=x_0$ .)

Second, one can also conjugate the inputs and outputs:

$\mathcal{F}^{-1}(\mathbf{x}) = \mathcal{F}(\mathbf{x}^*)^* / N$

Third, a variant of this conjugation trick, which is sometimes preferable because it requires no modification of the data values, involves swapping real and imaginary parts (which can be done on a computer simply by modifying pointers). Define swap( $x_n$ ) as $x_n$ with its real and imaginary parts swapped—that is, if $x_n = a + b i$ then swap( $x_n$ ) is $b + a i$ . Equivalently, swap( $x_n$ ) equals $i x_n^*$ . Then

$\mathcal{F}^{-1}(\mathbf{x}) = \textrm{swap}(\mathcal{F}(\textrm{swap}(\mathbf{x}))) / N$

That is, the inverse transform is the same as the forward transform with the real and imaginary parts swapped for both input and output, up to a normalization (Duhamel et al., 1988).

The conjugation trick can also be used to define a new transform, closely related to the DFT, that is involutary—that is, which is its own inverse. In particular, $T(\mathbf{x}) = \mathcal{F}(\mathbf{x}^*) / \sqrt{N}$ is clearly its own inverse: $T(T(\mathbf{x})) = \mathbf{x}$ . A closely related involutary transformation (by a factor of (1+i) /√2) is $H(\mathbf{x}) = \mathcal{F}((1+i) \mathbf{x}^*) / \sqrt{2N}$ , since the $(1+i)$ factors in $H(H(\mathbf{x}))$ cancel the 2. For real inputs $\mathbf{x}$ , the real part of $H(\mathbf{x})$ is none other than the discrete Hartley transform, which is also involutary.

[edit]Eigenvalues and eigenvectors

The eigenvalues of the DFT matrix are simple and well-known, whereas the eigenvectors are complicated, not unique, and are the subject of ongoing research.

Consider the unitary form $\mathbf{U}$ defined above for the DFT of length N, where

$\mathbf{U}_{m,n} = \frac1{\sqrt{N}}\omega_N^{(m-1)(n-1)} = \frac1{\sqrt{N}}e^{-\frac{2\pi i}N (m-1)(n-1)}.$

This matrix satisfies the matrix polynomial equation:

$\mathbf{U}^4 = \mathbf{I}.$

This can be seen from the inverse properties above: operating $\mathbf{U}$ twice gives the original data in reverse order, so operating $\mathbf{U}$ four times gives back the original data and is thus the identity matrix. This means that the eigenvalues $\lambda$ satisfy the equation:

$\lambda^4 = 1.$

Therefore, the eigenvalues of $\mathbf{U}$ are the fourth roots of unity: $\lambda$ is +1, −1, +i, or −i.

Since there are only four distinct eigenvalues for this $N\times N$ matrix, they have some multiplicity. The multiplicity gives the number of linearly independent eigenvectors corresponding to each eigenvalue. (Note that there are N independent eigenvectors; a unitary matrix is never defective.)

The problem of their multiplicity was solved by McClellan and Parks (1972), although it was later shown to have been equivalent to a problem solved by Gauss (Dickinson and Steiglitz, 1982). The multiplicity depends on the value of N modulo 4, and is given by the following table:

size N	λ = +1	λ = −1	λ = -i	λ = +i
4m	m + 1	m	m	m − 1
4m + 1	m + 1	m	m	m
4m + 2	m + 1	m + 1	m	m
4m + 3	m + 1	m + 1	m + 1	m
Multiplicities of the eigenvalues λ of the unitary DFT matrix U as a function of the transform size N (in terms of an integer m).

Otherwise stated, the characteristic polynomial of $\mathbf{U}$ is:

$\det (\lambda I - \mathbf{U})= (\lambda-1)^{\left\lfloor \tfrac {N+4}{4}\right\rfloor} (\lambda+1)^{\left\lfloor \tfrac {N+2}{4}\right\rfloor} (\lambda+i)^{\left\lfloor \tfrac {N+1}{4}\right\rfloor} (\lambda-i)^{\left\lfloor \tfrac {N-1}{4}\right\rfloor}.$

No simple analytical formula for general eigenvectors is known. Moreover, the eigenvectors are not unique because any linear combination of eigenvectors for the same eigenvalue is also an eigenvector for that eigenvalue. Various researchers have proposed different choices of eigenvectors, selected to satisfy useful properties like orthogonality and to have "simple" forms (e.g., McClellan and Parks, 1972; Dickinson and Steiglitz, 1982; Grünbaum, 1982; Atakishiyev and Wolf, 1997; Candan et al., 2000; Hanna et al., 2004; Gurevich and Hadani, 2008).

A straightforward approach is to discretize the eigenfunction of the continuous Fourier transform, namely the Gaussian function. Since periodic summation of the function means discretizing its frequency spectrum and discretization means periodic summation of the spectrum, the discretized and periodically summed Gaussian function yields an eigenvector of the discrete transform:

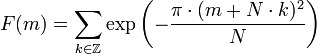§ $F(m) = \sum_{k\in\mathbb{Z}} \exp\left(-\frac{\pi\cdot(m+N\cdot k)^2}{N}\right)$ .

A closed form expression for the series is not known, but it converges rapidly.

Two other simple closed-form analytical eigenvectors for special DFT period N were found (Kong, 2008):

For DFT period N = 2L + 1 = 4K +1, where K is an integer, the following is an eigenvector of DFT:

§ $F(m)=\prod_{s=K+1}^L\left[\cos\left(\frac{2\pi}{N}m\right)- \cos\left(\frac{2\pi}{N}s\right)\right]$

For DFT period N = 2L = 4K, where K is an integer, the following is an eigenvector of DFT:

§ $F(m)=\sin\left(\frac{2\pi}{N}m\right)\prod_{s=K+1}^{L-1}\left[\cos\left(\frac{2\pi}{N}m\right)- \cos\left(\frac{2\pi}{N}s\right)\right]$

The choice of eigenvectors of the DFT matrix has become important in recent years in order to define a discrete analogue of the fractional Fourier transform—the DFT matrix can be taken to fractional powers by exponentiating the eigenvalues (e.g., Rubio and Santhanam, 2005). For the continuous Fourier transform, the natural orthogonal eigenfunctions are the Hermite functions, so various discrete analogues of these have been employed as the eigenvectors of the DFT, such as the Kravchuk polynomials (Atakishiyev and Wolf, 1997). The "best" choice of eigenvectors to define a fractional discrete Fourier transform remains an open question, however.

[edit]Uncertainty principle

If the random variable $X_k$ is constrained by:

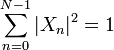
$\sum_{n=0}^{N-1}|X_n|^2=1$

then $P_n=|X_n|^2$ may be considered to represent a discrete probability mass function of n, with an associated probability mass function constructed from the transformed variable:

$Q_m=N|x_m|^2$

For the case of continuous functions P(x) and Q(k), the Heisenberg uncertainty principle states that:

$D_0(X)D_0(x)\ge\frac{1}{16\pi^2}$

where $D_0(X)$ and $D_0(x)$ are the variances of $|X|^2$ and $|x|^2$ respectively, with the equality attained in the case of a suitably normalized Gaussian distribution. Although the variances may be analogously defined for the DFT, an analogous uncertainty principle is not useful, because the uncertainty will not be shift-invariant. Nevertheless, a meaningful uncertainty principle has been introduced by Massar and Spindel.^[2]

However, the Hirschman uncertainty will have a useful analog for the case of the DFT.^[3] The Hirschman uncertainty principle is expressed in terms of the Shannon entropy of the two probability functions. In the discrete case, the Shannon entropies are defined as:

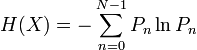
$H(X)=-\sum_{n=0}^{N-1} P_n\ln P_n$

and

$H(x)=-\sum_{m=0}^{N-1} Q_m\ln Q_m$

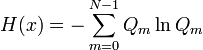
and the Hirschman uncertainty principle becomes:^[3]

$H(X)+H(x) \ge \ln(N)$

The equality is obtained for $P_n$ equal to translations and modulations of a suitably normalized Kronecker comb of period A where A is any exact integer divisor of N. The probability mass function $Q_m$ will then be proportional to a suitably translated Kronecker comb of period B=N/A.^[3]

[edit]The real-input DFT

If $x_0, \ldots, x_{N-1}$ are real numbers, as they often are in practical applications, then the DFT obeys the symmetry:

$X_{N-k} \equiv X_{-k} = X_k^*,$ where $X^*\,$ denotes complex conjugation.

It follows that X₀ and X_N/2 are real-valued, and the remainder of the DFT is completely specified by just N/2-1 complex numbers.

[edit]Generalized DFT (shifted and non-linear phase)

It is possible to shift the transform sampling in time and/or frequency domain by some real shifts a and b, respectively. This is sometimes known as a generalized DFT (orGDFT), also called the shifted DFT or offset DFT, and has analogous properties to the ordinary DFT:

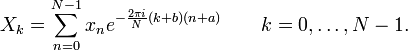
$X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{2 \pi i}{N} (k+b) (n+a)} \quad \quad k = 0, \dots, N-1.$

Most often, shifts of $1/2$ (half a sample) are used. While the ordinary DFT corresponds to a periodic signal in both time and frequency domains, $a=1/2$ produces a signal that is anti-periodic in frequency domain ( $X_{k+N} = - X_k$ ) and vice-versa for $b=1/2$ . Thus, the specific case of $a = b = 1/2$ is known as an odd-time odd-frequencydiscrete Fourier transform (or O² DFT). Such shifted transforms are most often used for symmetric data, to represent different boundary symmetries, and for real-symmetric data they correspond to different forms of the discrete cosine and sine transforms.

Another interesting choice is $a=b=-(N-1)/2$ , which is called the centered DFT (or CDFT). The centered DFT has the useful property that, when N is a multiple of four, all four of its eigenvalues (see above) have equal multiplicities (Rubio and Santhanam, 2005)^[4]

The term GDFT is also used for the non-linear phase extensions of DFT. Hence, GDFT method provides a generalization for constant amplitude orthogonal block transforms including linear and non-linear phase types. GDFT is a framework to improve time and frequency domain properties of the traditional DFT, e.g. auto/cross-correlations, by the addition of the properly designed phase shaping function (non-linear, in general) to the original linear phase functions (Akansu and Agirman-Tosun, 2010).^[5]

The discrete Fourier transform can be viewed as a special case of the z-transform, evaluated on the unit circle in the complex plane; more general z-transforms correspond tocomplex shifts a and b above.

[edit]Multidimensional DFT

The ordinary DFT transforms a one-dimensional sequence or array $x_n$ that is a function of exactly one discrete variable n. The multidimensional DFT of a multidimensional array $x_{n_1, n_2, \dots, n_d}$ that is a function of d discrete variables $n_\ell = 0, 1, \dots, N_\ell-1$ for $\ell$ in $1, 2, \dots, d$ is defined by:

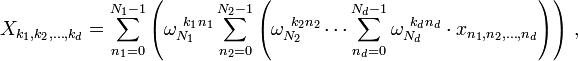
$X_{k_1, k_2, \dots, k_d} = \sum_{n_1=0}^{N_1-1} \left(\omega_{N_1}^{~k_1 n_1} \sum_{n_2=0}^{N_2-1} \left( \omega_{N_2}^{~k_2 n_2} \cdots \sum_{n_d=0}^{N_d-1} \omega_{N_d}^{~k_d n_d}\cdot x_{n_1, n_2, \dots, n_d} \right) \right) \, ,$

where $\omega_{N_\ell} = \exp(-2\pi i/N_\ell)$ as above and the d output indices run from $k_\ell = 0, 1, \dots, N_\ell-1$ . This is more compactly expressed in vector notation, where we define $\mathbf{n} = (n_1, n_2, \dots, n_d)$ and $\mathbf{k} = (k_1, k_2, \dots, k_d)$ as d-dimensional vectors of indices from 0 to $\mathbf{N} - 1$ , which we define as $\mathbf{N} - 1 = (N_1 - 1, N_2 - 1, \dots, N_d - 1)$ :

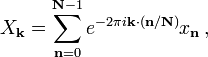
$X_\mathbf{k} = \sum_{\mathbf{n}=0}^{\mathbf{N}-1} e^{-2\pi i \mathbf{k} \cdot (\mathbf{n} / \mathbf{N})} x_\mathbf{n} \, ,$

where the division $\mathbf{n} / \mathbf{N}$ is defined as $\mathbf{n} / \mathbf{N} = (n_1/N_1, \dots, n_d/N_d)$ to be performed element-wise, and the sum denotes the set of nested summations above.

The inverse of the multi-dimensional DFT is, analogous to the one-dimensional case, given by:

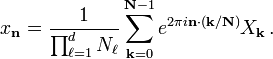
$x_\mathbf{n} = \frac{1}{\prod_{\ell=1}^d N_\ell} \sum_{\mathbf{k}=0}^{\mathbf{N}-1} e^{2\pi i \mathbf{n} \cdot (\mathbf{k} / \mathbf{N})} X_\mathbf{k} \, .$

As the one-dimensional DFT expresses the input $x_n$ as a superposition of sinusoids, the multidimensional DFT expresses the input as a superposition of plane waves, or multidimensional sinusoids. The direction of oscillation in space is $\mathbf{k} / \mathbf{N}$ . The amplitudes are $X_\mathbf{k}$ . This decomposition is of great importance for everything from digital image processing (two-dimensional) to solving partial differential equations. The solution is broken up into plane waves.

The multidimensional DFT can be computed by the composition of a sequence of one-dimensional DFTs along each dimension. In the two-dimensional case $x_{n_1,n_2}$ the $N_1$ independent DFTs of the rows (i.e., along $n_2$ ) are computed first to form a new array $y_{n_1,k_2}$ . Then the $N_2$ independent DFTs of y along the columns (along $n_1$ ) are computed to form the final result $X_{k_1,k_2}$ . Alternatively the columns can be computed first and then the rows. The order is immaterial because the nested summations above commute.

An algorithm to compute a one-dimensional DFT is thus sufficient to efficiently compute a multidimensional DFT. This approach is known as the row-column algorithm. There are also intrinsically multidimensional FFT algorithms.

[edit]The real-input multidimensional DFT

For input data $x_{n_1, n_2, \dots, n_d}$ consisting of real numbers, the DFT outputs have a conjugate symmetry similar to the one-dimensional case above:

$X_{k_1, k_2, \dots, k_d} = X_{N_1 - k_1, N_2 - k_2, \dots, N_d - k_d}^* ,$

where the star again denotes complex conjugation and the $\ell$ -th subscript is again interpreted modulo $N_\ell$ (for $\ell = 1,2,\ldots,d$ ).

[edit]Applications

The DFT has seen wide usage across a large number of fields; we only sketch a few examples below (see also the references at the end). All applications of the DFT depend crucially on the availability of a fast algorithm to compute discrete Fourier transforms and their inverses, a fast Fourier transform.

[edit]Spectral analysis

When the DFT is used for spectral analysis, the $\{x_n\}\,$ sequence usually represents a finite set of uniformly spaced time-samples of some signal $x(t)\,$ , where t represents time. The conversion from continuous time to samples (discrete-time) changes the underlying Fourier transform of x(t) into a discrete-time Fourier transform (DTFT), which generally entails a type of distortion called aliasing. Choice of an appropriate sample-rate (see Nyquist rate) is the key to minimizing that distortion. Similarly, the conversion from a very long (or infinite) sequence to a manageable size entails a type of distortion called leakage, which is manifested as a loss of detail (aka resolution) in the DTFT. Choice of an appropriate sub-sequence length (see Coherent sampling) is the primary key to minimizing that effect. When the available data (and time to process it) is more than the amount needed to attain the desired frequency resolution, a standard technique is to perform multiple DFTs, for example to create a spectrogram. If the desired result is a power spectrum and noise or randomness is present in the data, averaging the magnitude components of the multiple DFTs is a useful procedure to reduce the variance of the spectrum (also called a periodogram in this context); two examples of such techniques are the Welch method and the Bartlett method; the general subject of estimating the power spectrum of a noisy signal is called spectral estimation.

A final source of distortion (or perhaps illusion) is the DFT itself, because it is just a discrete sampling of the DTFT, which is a function of a continuous frequency domain. That can be mitigated by increasing the resolution of the DFT. That procedure is illustrated in the discrete-time Fourier transform article.

§ The procedure is sometimes referred to as zero-padding, which is a particular implementation used in conjunction with the fast Fourier transform (FFT) algorithm. The inefficiency of performing multiplications and additions with zero-valued "samples" is more than offset by the inherent efficiency of the FFT.

§ As already noted, leakage imposes a limit on the inherent resolution of the DTFT. So there is a practical limit to the benefit that can be obtained from a fine-grained DFT.

[edit]Data compression

The field of digital signal processing relies heavily on operations in the frequency domain (i.e. on the Fourier transform). For example, several lossy image and sound compression methods employ the discrete Fourier transform: the signal is cut into short segments, each is transformed, and then the Fourier coefficients of high frequencies, which are assumed to be unnoticeable, are discarded. The decompressor computes the inverse transform based on this reduced number of Fourier coefficients. (Compression applications often use a specialized form of the DFT, the discrete cosine transform or sometimes the modified discrete cosine transform.)

[edit]Partial differential equations

Discrete Fourier transforms are often used to solve partial differential equations, where again the DFT is used as an approximation for the Fourier series (which is recovered in the limit of infinite N). The advantage of this approach is that it expands the signal in complex exponentials e^inx, which are eigenfunctions of differentiation: d/dx e^inx = in e^inx. Thus, in the Fourier representation, differentiation is simple—we just multiply by i n. (Note, however, that the choice of n is not unique due to aliasing; for the method to be convergent, a choice similar to that in the trigonometric interpolation section above should be used.) A linear differential equation with constant coefficients is transformed into an easily solvable algebraic equation. One then uses the inverse DFT to transform the result back into the ordinary spatial representation. Such an approach is called a spectral method.

[edit]Polynomial multiplication

Suppose we wish to compute the polynomial product c(x) = a(x) · b(x). The ordinary product expression for the coefficients of c involves a linear (acyclic) convolution, where indices do not "wrap around." This can be rewritten as a cyclic convolution by taking the coefficient vectors for a(x) and b(x) with constant term first, then appending zeros so that the resultant coefficient vectors a and b have dimension d > deg(a(x)) + deg(b(x)). Then,

$\mathbf{c} = \mathbf{a} * \mathbf{b}$

Where c is the vector of coefficients for c(x), and the convolution operator $*\,$ is defined so

$c_n = \sum_{m=0}^{d-1}a_m b_{n-m\ \mathrm{mod}\ d} \qquad\qquad\qquad n=0,1\dots,d-1$

But convolution becomes multiplication under the DFT:

$\mathcal{F}(\mathbf{c}) = \mathcal{F}(\mathbf{a})\mathcal{F}(\mathbf{b})$

Here the vector product is taken elementwise. Thus the coefficients of the product polynomial c(x) are just the terms 0, ..., deg(a(x)) + deg(b(x)) of the coefficient vector

$\mathbf{c} = \mathcal{F}^{-1}(\mathcal{F}(\mathbf{a})\mathcal{F}(\mathbf{b})).$

With a fast Fourier transform, the resulting algorithm takes O (N log N) arithmetic operations. Due to its simplicity and speed, the Cooley–Tukey FFT algorithm, which is limited tocomposite sizes, is often chosen for the transform operation. In this case, d should be chosen as the smallest integer greater than the sum of the input polynomial degrees that is factorizable into small prime factors (e.g. 2, 3, and 5, depending upon the FFT implementation).

[edit]Multiplication of large integers

The fastest known algorithms for the multiplication of very large integers use the polynomial multiplication method outlined above. Integers can be treated as the value of a polynomial evaluated specifically at the number base, with the coefficients of the polynomial corresponding to the digits in that base. After polynomial multiplication, a relatively low-complexity carry-propagation step completes the multiplication.

[edit]Some discrete Fourier transform pairs

Some DFT pairs
$x_n = \frac{1}{N}\sum_{k=0}^{N-1}X_k e^{i 2 \pi kn/N}$	$X_k = \sum_{n=0}^{N-1}x_n e^{-i 2 \pi kn/N}$	Note
$x_n e^{i 2 \pi n\ell/N} \,$	$X_{k-\ell}\,$	Shift theorem
$x_{n-\ell}\,$	$X_k e^{-i 2 \pi k\ell/N} \,$	Shift theorem
$x_n \in \mathbb{R}$	$X_k=X_{N-k}^*\,$	Real DFT
$a^n\,$	$\left\{ \begin{matrix} N & \mbox{if } a = e^{i 2 \pi k/N} \\ \frac{1-a^N}{1-a \, e^{-i 2 \pi k/N} } & \mbox{otherwise} \end{matrix} \right.$	from the geometric progression formula
${N-1 \choose n}\,$	$\left(1+e^{-i 2 \pi k/N} \right)^{N-1}\,$	from the binomial theorem
$\left\{ \begin{matrix} \frac{1}{W} & \mbox{if } 2n < W \mbox{ or } 2(N-n) < W \\ 0 & \mbox{otherwise} \end{matrix} \right.$	$\left\{ \begin{matrix} 1 & \mbox{if } k = 0 \\ \frac{\sin\left(\frac{\pi W k}{N}\right)} {W \sin\left(\frac{\pi k}{N}\right)} & \mbox{otherwise} \end{matrix} \right.$	$x_n$ is a rectangular window function of W points centered on n=0, whereW is an odd integer, and $X_k$ is a sinc-like function (specifically, $X_k$ is aDirichlet kernel)
$\sum_{j\in\mathbb{Z}} \exp\left(-\frac{\pi}{cN}\cdot(n+N\cdot j)^2\right)$	$cN \cdot \sum_{j\in\mathbb{Z}} \exp\left(-\frac{\pi c}{N}\cdot(k+N\cdot j)^2\right)$	Discretization and periodic summation of the scaled Gaussian functionsfor $c>0$ . Since either $c$ or $\frac{1}{c}$ is larger than one and thus warrants fast convergence of one of the two series, for large $c$ you may choose to compute the frequency spectrum and convert to the time domain using the discrete Fourier transform.

[edit]Generalizations

[edit]Representation theory

For more details on this topic, see Representation theory of finite groups#Discrete Fourier transform.

The DFT can be interpreted as the complex-valued representation theory of the finite cyclic group. In other words, a sequence of n complex numbers can be thought of as an element of n-dimensional complex space Cⁿ or equivalently a function from the finite cyclic group of order n to the complex numbers, Z_n → C This latter may be suggestively written $\mathbf{C}^{\mathbf{Z}_n}$ to emphasize that this is a complex vector space whose coordinates are indexed by the n-element set Z_n.

From this point of view, one may generalize the DFT to representation theory generally, or more narrowly to the representation theory of finite groups.

More narrowly still, one may generalize the DFT by either changing the target (taking values in a field other than the complex numbers), or the domain (a group other than a finite cyclic group), as detailed in the sequel.

[edit]Other fields

Main articles: Discrete Fourier transform (general) and Number-theoretic transform

Many of the properties of the DFT only depend on the fact that $e^{-\frac{2 \pi i}{N}}$ is a primitive root of unity, sometimes denoted $\omega_N$ or $W_N$ (so that $\omega_N^N = 1$ ). Such properties include the completeness, orthogonality, Plancherel/Parseval, periodicity, shift, convolution, and unitarity properties above, as well as many FFT algorithms. For this reason, the discrete Fourier transform can be defined by using roots of unity in fields other than the complex numbers, and such generalizations are commonly called number-theoretic transforms(NTTs) in the case of finite fields. For more information, see number-theoretic transform and discrete Fourier transform (general).

[edit]Other finite groups

Main article: Fourier transform on finite groups

The standard DFT acts on a sequence x₀, x₁, …, x_N₋₁ of complex numbers, which can be viewed as a function {0, 1, …, N − 1} → C. The multidimensional DFT acts on multidimensional sequences, which can be viewed as functions

$\{0, 1, \ldots, N_1-1\} \times \cdots \times \{0, 1, \ldots, N_d-1\} \to \mathbb{C}.$

This suggests the generalization to Fourier transforms on arbitrary finite groups, which act on functions G → C where G is a finite group. In this framework, the standard DFT is seen as the Fourier transform on a cyclic group, while the multidimensional DFT is a Fourier transform on a direct sum of cyclic groups.

[edit]Alternatives

Main article: Discrete wavelet transform

For more details on this topic, see Discrete wavelet transform#Comparison with Fourier transform.

There are various alternatives to the DFT for various applications, prominent among which are wavelets. The analog of the DFT is the discrete wavelet transform (DWT). From the point of view of time–frequency analysis, a key limitation of the Fourier transform is that it does not include location information, only frequency information, and thus has difficulty in representing transients. As wavelets have location as well as frequency, they are better able to represent location, at the expense of greater difficulty representing frequency. For details, see comparison of the discrete wavelet transform with the discrete Fourier transform.