Logarithm

From Wikipedia, the free encyclopedia

The graph of the logarithm to base 2 crosses the x axis(horizontal axis) at 1 and passes through the points withcoordinates (2, 1), (4, 2), and (8, 3). For example, log₂(8) = 3, because 2³ = 8. The graph gets arbitrarily close to the y axis, but does not meet or intersect it.

The logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3:1000 = 10 × 10 × 10 = 10³. More generally, if x = b^y, then y is the logarithm of x to base b, and is written y = log_b(x), so log₁₀(1000) = 3.

The logarithm to base b = 10 is called the common logarithm and has many applications in science and engineering. The natural logarithm has the constant e (≈ 2.718) as its base; its use is widespread in pure mathematics, especially calculus. The binary logarithm uses base b = 2 and is prominent in computer science.

Logarithms were introduced by John Napier in the early 17th century as a means to simplify calculations. They were rapidly adopted by navigators, scientists, engineers, and others to perform computations more easily, usingslide rules and logarithm tables. Tedious multi-digit multiplication steps can be replaced by table look-ups and simpler addition because of the fact — important in its own right — that the logarithm of a product is the sum of the logarithms of the factors:

$\log_b(xy) = \log_b (x) + \log_b (y). \,$

The present-day notion of logarithms comes from Leonhard Euler, who connected them to the exponential functionin the 18th century.

Logarithmic scales reduce wide-ranging quantities to smaller scopes. For example, the decibel is a logarithmic unit quantifying sound pressure and voltage ratios. In chemistry, pH is a logarithmic measure for the acidity of anaqueous solution. Logarithms are commonplace in scientific formulae, and in measurements of the complexity of algorithms and of geometric objects called fractals. They describe musical intervals, appear in formulae counting prime numbers, inform some models in psychophysics, and can aid in forensic accounting.

In the same way as the logarithm reverses exponentiation, the complex logarithm is the inverse function of the exponential function applied to complex numbers. Thediscrete logarithm is another variant; it has applications in public-key cryptography.

[hide]

· 1 Motivation and definition

o 1.1 Exponentiation

o 1.2 Definition

o 1.3 Examples

· 2 Logarithmic identities

o 2.1 Product, quotient, power, and root

o 2.2 Change of base

· 3 Particular bases

· 4 History

o 4.1 Predecessors

o 4.2 From Napier to Euler

o 4.3 Logarithm tables, slide rules, and historical applications

· 5 Analytic properties

o 5.1 Logarithmic function

o 5.2 Inverse function

o 5.3 Derivative and antiderivative

o 5.4 Integral representation of the natural logarithm

o 5.5 Transcendence of the logarithm

· 6 Calculation

o 6.1 Power series

o 6.2 Arithmetic-geometric mean approximation

· 7 Applications

o 7.1 Logarithmic scale

o 7.2 Psychology

o 7.3 Probability theory and statistics

o 7.4 Computational complexity

o 7.5 Entropy and chaos

o 8.1 Complex logarithm

o 8.2 Inverses of other exponential functions

o 8.3 Related concepts

· 9 See also

· 10 Notes

· 11 References

· 12 External links

[edit]Motivation and definition

The idea of logarithms is to reverse the operation of exponentiation, that is raising a number to a power. For example, the third power (or cube) of 2 is 8, because 8 is the product of three factors of 2:

$2^3 = 2 \times 2 \times 2 = 8. \,$

It follows that the logarithm of 8 with respect to base 2 is 3, so log₂ 8 = 3.

[edit]Exponentiation

The third power of some number b is the product of three factors of b. More generally, raising b to the n-th power, where n is a natural number, is done by multiplying nfactors of b. The n-th power of b is written bⁿ, so that

$b^n = \underbrace{b \times b \times \cdots \times b}_{n \text{ factors}}.$

Exponentation may be extended to b^y, where b is a positive number and the exponent y is any real number. For example, b⁻¹ is the reciprocal of b, that is, 1/b.^{[nb 1]}

[edit]Definition

The logarithm of a number x with respect to base b is the exponent by which b must be raised to yield x. In other words, the logarithm of x to base b is the solution y to the equation^[2]

$b^y = x. \,$

The logarithm is denoted "log_b(x)" (pronounced as "the logarithm of x to base b" or "the base-b logarithm of x"). In the equation y = log_b(x), the value y is the answer to the question "To what power must b be raised, in order to yield x?". To define the logarithm, the base b must be a positive real number not equal to 1 and x must be a positive number.^{[nb 2]}

[edit]Examples

For example, log₂(16) = 4, since 2⁴ = 2 ×2 × 2 × 2 = 16. Logarithms can also be negative:

$\log_2 \!\left( \frac{1}{2} \right) = -1,\,$

since

$2^{-1} = \frac 1 {2^1} = \frac 1 2.$

A third example: log₁₀(150) is approximately 2.176, which lies between 2 and 3, just as 150 lies between 10² = 100 and 10³ = 1000. Finally, for any base b, log_b(b) = 1and log_b(1) = 0, since b¹ = b and b⁰ = 1, respectively.

[edit]Logarithmic identities

Main article: List of logarithmic identities

Several important formulas, sometimes called logarithmic identities or log laws, relate logarithms to one another.^[3]

[edit]Product, quotient, power, and root

The logarithm of a product is the sum of the logarithms of the numbers being multiplied; the logarithm of the ratio of two numbers is the difference of the logarithms. The logarithm of the p-th power of a number is p times the logarithm of the number itself; the logarithm of a p-th root is the logarithm of the number divided by p. The following table lists these identities with examples:

	Formula	Example
product	$\log_b(x y) = \log_b (x) + \log_b (y) \,$	$\log_3 (243) = \log_3(9 \cdot 27) = \log_3 (9) + \log_3 (27) = 2 + 3 = 5 \,$
quotient	$\log_b \!\left(\frac x y \right) = \log_b (x) - \log_b (y) \,$	$\log_2 (16) = \log_2 \!\left ( \frac{64}{4} \right ) = \log_2 (64) - \log_2 (4) = 6 - 2 = 4$
power	$\log_b(x^p) = p \log_b (x) \,$	$\log_2 (64) = \log_2 (2^6) = 6 \log_2 (2) = 6 \,$
root	$\log_b \sqrt[p]{x} = \frac {\log_b (x)} p \,$	$\log_{10} \sqrt{1000} = \frac{1}{2}\log_{10} 1000 = \frac{3}{2} = 1.5$

[edit]Change of base

The logarithm log_b(x) can be computed from the logarithms of x and b with respect to an arbitrary base k using the following formula:

$\log_b(x) = \frac{\log_k(x)}{\log_k(b)}.\,$

Typical scientific calculators calculate the logarithms to bases 10 and e.^[4] Logarithms with respect to any base b can be determined using either of these two logarithms by the previous formula:

$\log_b (x) = \frac{\log_{10} (x)}{\log_{10} (b)} = \frac{\log_{e} (x)}{\log_{e} (b)}. \,$

Given a number x and its logarithm log_b(x) to an unknown base b, the base is given by:

$b = x^\frac{1}{\log_b(x)}.$

[edit]Particular bases

Among all choices for the base b, three are particularly common. These are b = 10, b = e (the irrational mathematical constant ≈ 2.71828), and b = 2. In mathematical analysis, the logarithm to base e is widespread because of its particular analytical properties explained below. On the other hand, base-10 logarithms are easy to use for manual calculations in the decimal number system:^[5]

$\log_{10}(10 x) = \log_{10}(10) + \log_{10}(x) = 1 + \log_{10}(x).\$

Thus, log₁₀(x) is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than log₁₀(x).^[6] For example, log₁₀(1430) is approximately 3.15. The next integer is 4, which is the number of digits of 1430. The logarithm to base two is used in computer science, where the binary system is ubiquitous.

The following table lists common notations for logarithms to these bases and the fields where they are used. Many disciplines write log(x) instead of log_b(x), when the intended base can be determined from the context. The notation ^blog(x) also occurs.^[7] The "ISO notation" column lists designations suggested by the International Organization for Standardization (ISO 31-11).^[8]

Base b	Name for log_b(x)	ISO notation	Other notations	Used in
2	binary logarithm	lb(x)^[9]	ld(x), log(x), lg(x)	computer science, information theory, mathematics
e	natural logarithm	ln(x)^{[nb 3]}	log(x) (in mathematics and many programming languages^{[nb 4]})	mathematical analysis, physics, chemistry, statistics, economics, and some engineering fields
10	common logarithm	lg(x)	log(x) (in engineering, biology, astronomy),	various engineering fields (see decibel and see below), logarithm tables, handheld calculators

[edit]History

[edit]Predecessors

The Babylonians sometime in 2000–1600 BC may have invented the quarter square multiplication algorithm to multiply two numbers using only addition, subtraction and a table of squares.^[13][14] However it could not be used for division without an additional table of reciprocals. Large tables of quarter squares were used to simplify the accurate multiplication of large numbers from 1817 onwards until this was superseded by the use of computers.

Michael Stifel published Arithmetica integra in Nuremberg in 1544, which contains a table^[15] of integers and powers of 2 that has been considered an early version of a logarithmic table.^[16][17]

In the 16th and early 17th centuries an algorithm called prosthaphaeresis was used to approximate multiplication and division. This used the trigonometric identity

$\cos\,\alpha\,\cos\,\beta = \frac12[\cos(\alpha+\beta) + \cos(\alpha-\beta)]$

or similar to convert the multiplications to additions and table lookups. However logarithms are more straightforward and require less work. It can be shown using complex numbers that this is basically the same technique.

[edit]From Napier to Euler

John Napier (1550–1617), the inventor of logarithms

The method of logarithms was publicly propounded by John Napier in 1614, in a book entitled Mirifici Logarithmorum Canonis Descriptio (Description of the Wonderful Rule of Logarithms).^[18] Joost Bürgi independently invented logarithms but published six years after Napier.^[19]

Johannes Kepler, who used logarithm tables extensively to compile his Ephemeris and therefore dedicated it to John Napier,^[20]remarked:

...the accent in calculation led Justus Byrgius [Joost Bürgi] on the way to these very logarithms many years before Napier's system appeared; but ...instead of rearing up his child for the public benefit he deserted it in the birth.

—Johannes Kepler^[21], Rudolphine Tables (1627)

By repeated subtractions Napier calculated (1 − 10⁻⁷)^L for L ranging from 1 to 100. The result for L=100 is approximately0.99999 = 1 − 10⁻⁵. Napier then calculated the products of these numbers with 10⁷(1 − 10⁻⁵)^L for L from 1 to 50, and did similarly with 0.9998 ≈ (1 − 10⁻⁵)²⁰ and 0.9 ≈ 0.995²⁰. These computations, which occupied 20 years, allowed him to give, for any number N from 5 to 10 million, the number L that solves the equation

$N=10^7 {(1-10^{-7})}^L. \,$

Napier first called L an "artificial number", but later introduced the word "logarithm" to mean a number that indicates a ratio:λόγος (logos) meaning proportion, and ἀριθμός (arithmos) meaning number. In modern notation, the relation to natural logarithms is: ^[22]

$L = \log_{(1-10^{-7})} \!\left( \frac{N}{10^7} \right) \approx 10^7 \log_{ \frac{1}{e}} \!\left( \frac{N}{10^7} \right) = -10^7 \log_e \!\left( \frac{N}{10^7} \right),$

where the very close approximation corresponds to the observation that

${(1-10^{-7})}^{10^7} \approx \frac{1}{e}. \,$

The invention was quickly and widely met with acclaim. The works of Bonaventura Cavalieri (Italy), Edmund Wingate (France), Xue Fengzuo (China), and Johannes Kepler'sChilias logarithmorum (Germany) helped spread the concept further.^[23]

The hyperbola y = 1/x (red curve) and the area from x = 1 to 6 (shaded in orange).

In 1647 Grégoire de Saint-Vincent related logarithms to the quadrature of the hyperbola, by pointing out that the area f(t) under the hyperbola from x = 1 to x = t satisfies

$f(tu) = f(t) + f(u).\,$

The natural logarithm was first described by Nicholas Mercator in his work Logarithmotechnia published in 1668,^[24] although the mathematics teacher John Speidell had already in 1619 compiled a table on the natural logarithm.^[25] Around 1730, Leonhard Euler defined the exponential function and the natural logarithm by

$e^x = \lim_{n \rightarrow \infty} (1+x/n)^n,$

$\ln(x) = \lim_{n \rightarrow \infty} n(x^{1/n} - 1).$

Euler also showed that the two functions are inverse to one another.^[26][27][28]

[edit]Logarithm tables, slide rules, and historical applications

The 1797 Encyclopædia Britannica explanation of logarithms

By simplifying difficult calculations, logarithms contributed to the advance of science, and especially of astronomy. They were critical to advances in surveying, celestial navigation, and other domains. Pierre-Simon Laplace called logarithms

"...[a]n admirable artifice which, by reducing to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust inseparable from long calculations."^[29]

A key tool that enabled the practical use of logarithms before calculators and computers was the table of logarithms.^[30] The first such table was compiled by Henry Briggs in 1617, immediately after Napier's invention. Subsequently, tables with increasing scope and precision were written. These tables listed the values of log_b(x) and b^x for any number x in a certain range, at a certain precision, for a certain baseb (usually b = 10). For example, Briggs' first table contained the common logarithms of all integers in the range 1–1000, with a precision of 8 digits. As the function f(x) = b^x is the inverse function of log_b(x), it has been called the antilogarithm.^[31] The product and quotient of two positive numbers c and d were routinely calculated as the sum and difference of their logarithms. The product cd or quotient c/d came from looking up the antilogarithm of the sum or difference, also via the same table:

$c d = b^{\log_b (c)} \, b^{\log_b (d)} = b^{\log_b (c) + \log_b (d)} \,$

and

$\frac c d = c d^{-1} = b^{\log_b (c) - \log_b (d)}. \,$

For manual calculations that demand any appreciable precision, performing the lookups of the two logarithms, calculating their sum or difference, and looking up the antilogarithm is much faster than performing the multiplication by earlier methods such as prosthaphaeresis, which relies on trigonometric identities. Calculations of powers and roots are reduced to multiplications or divisions and look-ups by

$c^d = (b^{\log_b (c) })^d = b^{d \log_b (c)} \,$

and

$\sqrt[d]{c} = c^{\frac 1 d} = b^{\frac{1}{d} \log_b (c)}. \,$

Many logarithm tables give logarithms by separately providing the characteristic and mantissa of x, that is to say, the integer part and the fractional part of log₁₀(x).^[32] The characteristic of 10 · x is one plus the characteristic of x, and their significands are the same. This extends the scope of logarithm tables: given a table listing log₁₀(x) for all integers x ranging from 1 to 1000, the logarithm of 3542 is approximated by

$\log_{10}(3542) = \log_{10}(10\cdot 354.2) = 1 + \log_{10}(354.2) \approx 1 + \log_{10}(354). \,$

Another critical application was the slide rule, a pair of logarithmically divided scales used for calculation, as illustrated here:

Schematic depiction of a slide rule. Starting from 2 on the lower scale, add the distance to 3 on the upper scale to reach the product 6. The slide rule works because it is marked such that the distance from 1 to x is proportional to the logarithm of x.

The non-sliding logarithmic scale, Gunter's rule, was invented shortly after Napier's invention. William Oughtred enhanced it to create the slide rule—a pair of logarithmic scales movable with respect to each other. Numbers are placed on sliding scales at distances proportional to the differences between their logarithms. Sliding the upper scale appropriately amounts to mechanically adding logarithms. For example, adding the distance from 1 to 2 on the lower scale to the distance from 1 to 3 on the upper scale yields a product of 6, which is read off at the lower part. The slide rule was an essential calculating tool for engineers and scientists until the 1970s, because it allows, at the expense of precision, much faster computation than techniques based on tables.^[26]

[edit]Analytic properties

A deeper study of logarithms requires the concept of a function. A function is a rule that, given one number, produces another number.^[33] An example is the function producing the x-th power of b from any real number x, where the base b is a fixed number. This function is written

$f(x) = b^x. \,$

[edit]Logarithmic function

To justify the definition of logarithms, it is necessary to show that the equation

$b^x = y \,$

has a solution x and that this solution is unique, provided that y is positive and that b is positive and unequal to 1. A proof of that fact requires the intermediate value theorem from elementary calculus.^[34] This theorem states that a continuous function that produces two values m and n also produces any value that lies between m and n. A function is continuous if it does not "jump", that is, if its graph can be drawn without lifting the pen.

This property can be shown to hold for the function f(x) = b^x. Because f takes arbitrarily large and arbitrarily small positive values, any number y > 0 lies between f(x₀) andf(x₁) for suitable x₀ and x₁. Hence, the intermediate value theorem ensures that the equation f(x) = y has a solution. Moreover, there is only one solution to this equation, because the function f is strictly increasing (for b > 1), or strictly decreasing (for 0 < b < 1).^[35]

The unique solution x is the logarithm of y to base b, log_b(y). The function that assigns to y its logarithm is called logarithm function or logarithmic function (or justlogarithm).

[edit]Inverse function

The graph of the logarithm function log_b(x) (blue) is obtained by reflecting the graph of the function b^x (red) at the diagonal line (x = y).

The formula for the logarithm of a power says in particular that for any number x,

$\log_b \left (b^x \right) = x \log_b(b) = x.$

In prose, taking the x-th power of b and then the base-b logarithm gives back x. Conversely, given a positive number y, the formula

$b^{\log_b(y)} = y$

says that first taking the logarithm and then exponentiating gives back y. Thus, the two possible ways of combining (orcomposing) logarithms and exponentiation give back the original number. Therefore, the logarithm to base b is the inverse function of f(x) = b^x.^[36]

Inverse functions are closely related to the original functions. Their graphs correspond to each other upon exchanging the x- and the y-coordinates (or upon reflection at the diagonal line x = y), as shown at the right: a point (t, u = b^t) on the graph of f yields a point (u, t = log_bu) on the graph of the logarithm and vice versa. As a consequence, log_b(x) diverges to infinity (gets bigger than any given number) if x grows to infinity, provided that b is greater than one. In that case, log_b(x) is an increasing function. Forb < 1, log_b(x) tends to minus infinity instead. When x approaches zero, log_b(x) goes to minus infinity for b > 1 (plus infinity forb < 1, respectively).

[edit]Derivative and antiderivative

The graph of the natural logarithm (green) and its tangent at x = 1.5 (black)

Analytic properties of functions pass to their inverses.^[34] Thus, as f(x) = b^x is a continuous and differentiable function, so is log_b(y). Roughly, a continuous function is differentiable if its graph has no sharp "corners". Moreover, as the derivative of f(x) evaluates to ln(b)b^x by the properties of the exponential function, the chain rule implies that the derivative of log_b(x) is given by^[35][37]

$\frac{d}{dx} \log_b(x) = \frac{1}{x\ln(b)}.$

That is, the slope of the tangent touching the graph of the base-b logarithm at the point (x, log_b(x)) equals 1/(x ln(b)). In particular, the derivative of ln(x) is 1/x, which implies that the antiderivative of 1/x is ln(x) + C. The derivative with a generalised functional argument f(x) is

$\frac{d}{dx} \ln(f(x)) = \frac{f'(x)}{f(x)}.$

The quotient at the right hand side is called the logarithmic derivative of f. Computing f'(x) by means of the derivative of ln(f(x)) is known as logarithmic differentiation.^[38] The antiderivative of the natural logarithm ln(x) is:^[39]

$\int \ln(x) \,dx = x \ln(x) - x + C.$

Related formulas, such as antiderivatives of logarithms to other bases can be derived from this equation using the change of bases.^[40]

[edit]Integral representation of the natural logarithm

The natural logarithm of t is the shaded area underneath the graph of the functionf(x) = 1/x (reciprocal of x).

The natural logarithm of t agrees with the integral of 1/x dx from 1 to t:

$\ln (t) = \int_1^t \frac{1}{x} \, dx.$

In other words, ln(t) equals the area between the x axis and the graph of the function 1/x, ranging from x = 1 to x = t (figure at the right). This is a consequence of the fundamental theorem of calculus and the fact that derivative of ln(x) is 1/x. The right hand side of this equation can serve as a definition of the natural logarithm. Product and power logarithm formulas can be derived from this definition.^[41] For example, the product formula ln(tu) = ln(t) + ln(u) is deduced as:

$\ln(tu) = \int_1^{tu} \frac{1}{x} \, dx \ \stackrel {(1)} = \int_1^{t} \frac{1}{x} \, dx + \int_t^{tu} \frac{1}{x} \, dx \ \stackrel {(2)} = \ln(t) + \int_1^u \frac{1}{w} \, dw = \ln(t) + \ln(u).$

The equality (1) splits the integral into two parts, while the equality (2) is a change of variable (w = x/t). In the illustration below, the splitting corresponds to dividing the area into the yellow and blue parts. Rescaling the left hand blue area vertically by the factor t and shrinking it by the same factor horizontally does not change its size. Moving it appropriately, the area fits the graph of the function f(x) = 1/x again. Therefore, the left hand blue area, which is the integral of f(x) from t to tu is the same as the integral from 1 to u. This justifies the equality (2) with a more geometric proof.

A visual proof of the product formula of the natural logarithm

The power formula ln(t^r) = r ln(t) may be derived in a similar way:

$\ln(t^r) = \int_1^{t^r} \frac{1}{x}dx = \int_1^t \frac{1}{w^r} \left(rw^{r - 1} \, dw\right) = r \int_1^t \frac{1}{w} \, dw = r \ln(t).$

The second equality uses a change of variables (integration by substitution), w = x^1/r.

The sum over the reciprocals of natural numbers,

$1 + \frac 1 2 + \frac 1 3 + \cdots + \frac 1 n = \sum_{k=1}^n \frac{1}{k},$

is called the harmonic series. It is closely tied to the natural logarithm: as n tends to infinity, the difference,

$\sum_{k=1}^n \frac{1}{k} - \ln(n),$

converges (i.e., gets arbitrarily close) to a number known as the Euler–Mascheroni constant. This relation aids in analyzing the performance of algorithms such asquicksort.^[42]

There is also another integral representation of the logarithm that is useful in some situations.

$\ln(x) = -\lim_{\epsilon \to 0} \int_\epsilon^\infty \frac{dt}{t}\left( e^{-xt} - e^{-t} \right)$

This can be verified by showing that it has the same value at x = 1, and the same derivative.

[edit]Transcendence of the logarithm

The logarithm is an example of a transcendental function and from a theoretical point of view, the Gelfond–Schneider theorem asserts that logarithms usually take "difficult" values. The formal statement relies on the notion of algebraic numbers, which includes all rational numbers, but also numbers such as the square root of 2 or

$\sqrt{-5+\sqrt[3]{3 / 13}}.$

Complex numbers that are not algebraic are called transcendental;^[43] for example, π and e are such numbers. Almost all complex numbers are transcendental. Using these notions, the Gelfond–Scheider theorem states that given two algebraic numbers a and b, log_b(a) is either a transcendental number or a rational number p / q (in which case a^q = b^p, so a and b were closely related to begin with).^[44]

[edit]Calculation

Logarithms are easy to compute in some cases, such as log₁₀(1,000) = 3. In general, logarithms can be calculated using power series or the arithmetic-geometric mean, or be retrieved from a precalculated logarithm table that provides a fixed precision.^[45][46] Newton's method, an iterative method to solve equations approximately, can also be used to calculate the logarithm, because its inverse function, the exponential function, can be computed efficiently.^[47] Using look-up tables, CORDIC-like methods can be used to compute logarithms if the only available operations are addition and bit shifts.^[48][49] Moreover, the binary logarithm algorithm calculates lb(x) recursively based on repeated squarings of x, taking advantage of the relation

$\log_2(x^2) = 2 \log_2 (x). \,$

[edit]Power series

Taylor series

The Taylor series of ln(z) centered at z = 1. The animation shows the first 10 approximations along with the 99th and 100th. The approximations do not converge beyond a distance of 1 from the center.

For any real number z that satisfies 0 < z < 2, the following formula holds:^{[nb 5][50]}

$\ln (z) = (z-1) - \frac{(z-1)^2}{2} + \frac{(z-1)^3}{3} - \frac{(z-1)^4}{4} + \cdots$

This is a shorthand for saying that ln(z) can be approximated to a more and more accurate value by the following expressions:

$\begin{array}{lllll} (z-1) & & \\ (z-1) & - & \frac{(z-1)^2}{2} & \\ (z-1) & - & \frac{(z-1)^2}{2} & + & \frac{(z-1)^3}{3} \\ \vdots & \end{array}$

For example, with z = 1.5 the third approximation yields 0.4167, which is about 0.011 greater than ln(1.5) = 0.405465. Thisseries approximates ln(z) with arbitrary precision, provided the number of summands is large enough. In elementary calculus, ln(z) is therefore the limit of this series. It is the Taylor series of the natural logarithm at z = 1. The Taylor series of ln z provides a particularly useful approximation to ln(1+z) when z is small, |z| << 1, since then

$\ln (1+z) = z - \frac{z^2}{2} + \cdots \approx z.$

For example, with z = 0.1 the first-order approximation gives ln(1.1) ≈ 0.1, which is less than 5% off the correct value 0.0953.

More efficient series

Another series is based on the area hyperbolic tangent function:

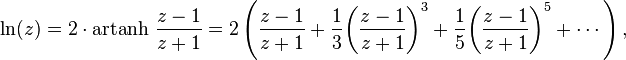
$\ln (z) = 2\cdot\operatorname{artanh}\,\frac{z-1}{z+1} = 2 \left ( \frac{z-1}{z+1} + \frac{1}{3}{\left(\frac{z-1}{z+1}\right)}^3 + \frac{1}{5}{\left(\frac{z-1}{z+1}\right)}^5 + \cdots \right ),$

for any real number z > 0.^{[nb 6][50]} Using the Sigma notation, this is also written as

$\ln (z) = 2\sum_{n=0}^\infty\frac{1}{2n+1}\left(\frac{z-1}{z+1}\right)^{2n+1}.$

This series can be derived from the above Taylor series. It converges more quickly than the Taylor series, especially if z is close to 1. For example, for z = 1.5, the first three terms of the second series approximate ln(1.5) with an error of about 3×10⁻⁶. The quick convergence for z close to 1 can be taken advantage of in the following way: given a low-accuracy approximation y ≈ ln(z) and putting

$A = \frac z{\exp(y)}, \,$

the logarithm of z is:

$\ln (z)=y+\ln (A). \,$

The better the initial approximation y is, the closer A is to 1, so its logarithm can be calculated efficiently. A can be calculated using the exponential series, which converges quickly provided y is not too large. Calculating the logarithm of larger z can be reduced to smaller values of z by writing z = a · 10^b, so thatln(z) = ln(a) + b · ln(10).

A closely related method can be used to compute the logarithm of integers. From the above series, it follows that:

$\ln (n+1) = \ln(n) + 2\sum_{k=0}^\infty\frac{1}{2k+1}\left(\frac{1}{2 n+1}\right)^{2k+1}.$

If the logarithm of a large integer n is known, then this series yields a fast converging series for log(n+1).

[edit]Arithmetic-geometric mean approximation

The arithmetic-geometric mean yields high precision approximations of the natural logarithm. ln(x) is approximated to a precision of 2^−p (or p precise bits) by the following formula (due to Carl Friedrich Gauss):^[51][52]

$\ln (x) \approx \frac{\pi}{2 M(1,2^{2-m}/x)} - m \ln (2).$

Here M denotes the arithmetic-geometric mean. It is obtained by repeatedly calculating the average (arithmetic mean) and the square root of the product of two numbers (geometric mean). Moreover, m is chosen such that

$x \,2^m > 2^{p/2}.\,$

Both the arithmetic-geometric mean and the constants π and ln(2) can be calculated with quickly converging series.

[edit]Applications

A nautilus displaying a logarithmic spiral

Logarithms have many applications inside and outside mathematics. Some of these occurrences are related to the notion ofscale invariance. For example, each chamber of the shell of a nautilus is an approximate copy of the next one, scaled by a constant factor. This gives rise to a logarithmic spiral.^[53] Benford's law on the distribution of leading digits can also be explained by scale invariance.^[54] Logarithms are also linked to self-similarity. For example, logarithms appear in the analysis of algorithms that solve a problem by dividing it into two similar smaller problems and patching their solutions.^[55] The dimensions of self-similar geometric shapes, that is, shapes whose parts resemble the overall picture are also based on logarithms. Logarithmic scales are useful for quantifying the relative change of a value as opposed to its absolute difference. Moreover, because the logarithmic function log(x) grows very slowly for large x, logarithmic scales are used to compress large-scale scientific data. Logarithms also occur in numerous scientific formulas, such as the Tsiolkovsky rocket equation, the Fenske equation, or theNernst equation.

[edit]Logarithmic scale

Main article: Logarithmic scale

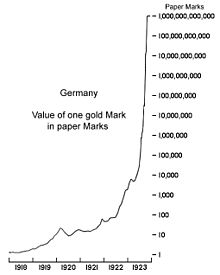
A logarithmic chart depicting the value of one Goldmark in Papiermarks during theGerman hyperinflation in the 1920s

Scientific quantities are often expressed as logarithms of other quantities, using a logarithmic scale. For example, the decibel is a logarithmic unit of measurement. It is based on the common logarithm of ratios — 10 times the common logarithm of a powerratio or 20 times the common logarithm of a voltage ratio. It is used to quantify the loss of voltage levels in transmitting electrical signals,^[56] to describe power levels of sounds in acoustics,^[57] and the absorbance of light in the fields of spectrometry andoptics. The signal-to-noise ratio describing the amount of unwanted noise in relation to a (meaningful) signal is also measured in decibels.^[58] In a similar vein, the peak signal-to-noise ratio is commonly used to assess the quality of sound and image compression methods using the logarithm.^[59]

The strength of an earthquake is measured by taking the common logarithm of the energy emitted at the quake. This is used in the moment magnitude scale or the Richter scale. For example, a 5.0 earthquake releases 10 times and a 6.0 releases 100 times the energy of a 4.0.^[60] Another logarithmic scale is apparent magnitude. It measures the brightness of stars logarithmically.^[61] Yet another example is pH in chemistry; pH is the negative of the common logarithm of the activity ofhydronium ions (the form hydrogen ions H⁺ take in water).^[62] The activity of hydronium ions in neutral water is 10⁻⁷ mol·L⁻¹, hence a pH of 7. Vinegar typically has a pH of about 3. The difference of 4 corresponds to a ratio of 10⁴ of the activity, that is, vinegar's hydronium ion activity is about 10⁻³ mol·L⁻¹.

Semilog (log-linear) graphs use the logarithmic scale concept for visualization: one axis, typically the vertical one, is scaled logarithmically. For example, the chart at the right compresses the steep increase from 1 million to 1 trillion to the same space (on the vertical axis) as the increase from 1 to 1 million. In such graphs, exponential functions of the form f(x) = a · b^x appear as straight lines with slope equal to the logarithm of b. Log-log graphs scale both axes logarithmically, which causes functions of the form f(x) = a · x^k to be depicted as straight lines with slope equal to the exponent k. This is applied in visualizing and analyzing power laws.^[63]

[edit]Psychology

Logarithms occur in several laws describing human perception:^[64][65] Hick's law proposes a logarithmic relation between the time individuals take for choosing an alternative and the number of choices they have.^[66] Fitts's law predicts that the time required to rapidly move to a target area is a logarithmic function of the distance to and the size of the target.^[67] In psychophysics, the Weber–Fechner law proposes a logarithmic relationship between stimulus and sensation such as the actual vs. the perceived weight of an item a person is carrying.^[68] (This "law", however, is less precise than more recent models, such as the Stevens' power law.^[69])

Psychological studies found that mathematically unsophisticated individuals tend to estimate quantities logarithmically, that is, they position a number on an unmarked line according to its logarithm, so that 10 is positioned as close to 20 as 100 is to 200. Increasing mathematical understanding shifts this to a linear estimate (positioning 100 10x as far away).^[70][71]

[edit]Probability theory and statistics

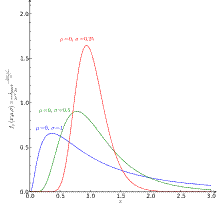
Three probability density functions (PDF) of random variables with log-normal distributions. The location parameter $μ$ , which is zero for all three of the PDFs shown, is the mean of the logarithm of the random variable, not the mean of the variable itself.

Distribution of first digits (in %, red bars) in the population of the 237 countries of the world. Black dots indicate the distribution predicted by Benford's law.

Logarithms arise in probability theory: the law of large numbers dictates that, for a fair coin, as the number of coin-tosses increases to infinity, the observed proportion of heads approaches one-half. The fluctuations of this proportion about one-half are described by the law of the iterated logarithm.^[72]

Logarithms also occur in log-normal distributions. When the logarithm of a random variable has a normal distribution, the variable is said to have a log-normal distribution.^[73] Log-normal distributions are encountered in many fields, wherever a variable is formed as the product of many independent positive random variables, for example in the study of turbulence.^[74]

Logarithms are used for maximum-likelihood estimation of parametric statistical models. For such a model, the likelihood function depends on at least one parameter that must be estimated. A maximum of the likelihood function occurs at the same parameter-value as a maximum of the logarithm of the likelihood (the "log likelihood"), because the logarithm is an increasing function. The log-likelihood is easier to maximize, especially for the multiplied likelihoods for independent random variables.^[75]

Benford's law describes the occurrence of digits in many data sets, such as heights of buildings. According to Benford's law, the probability that the first decimal-digit of an item in the data sample is d (from 1 to 9) equals log₁₀(d + 1) − log₁₀(d), regardless of the unit of measurement.^[76] Thus, about 30% of the data can be expected to have 1 as first digit, 18% start with 2, etc. Auditors examine deviations from Benford's law to detect fraudulent accounting.^[77]

[edit]Computational complexity

Analysis of algorithms is a branch of computer science that studies the performance of algorithms (computer programs solving a certain problem).^[78] Logarithms are valuable for describing algorithms that divide a problem into smaller ones, and join the solutions of the subproblems.^[79]

For example, to find a number in a sorted list, the binary search algorithm checks the middle entry and proceeds with the half before or after the middle entry if the number is still not found. This algorithm requires, on average, log₂(N) comparisons, where Nis the list's length.^[80] Similarly, the merge sort algorithm sorts an unsorted list by dividing the list into halves and sorting these first before merging the results. Merge sort algorithms typically require a time approximately proportional to N · log(N).^[81] The base of the logarithm is not specified here, because the result only changes by a constant factor when another base is used. A constant factor, is usually disregarded in the analysis of algorithms under the standard uniform cost model.^[82]

A function f(x) is said to grow logarithmically if f(x) is (exactly or approximately) proportional to the logarithm of x. (Biological descriptions of organism growth, however, use this term for an exponential function.^[83]) For example, any natural number N can be represented in binary form in no more than log₂(N) + 1 bits. In other words, the amount of memory needed to store N grows logarithmically with N.

[edit]Entropy and chaos

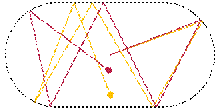
Billiards on an oval billiard table. Two particles, starting at the center with an angle differing by one degree, take paths that diverge chaotically because of reflections at the boundary.

Entropy is broadly a measure of the disorder of some system. In statistical thermodynamics, the entropy S of some physical system is defined as

$S = - k \sum_i p_i \ln(p_i).\,$

The sum is over all possible states i of the system in question, such as the positions of gas particles in a container. Moreover,p_i is the probability that the state i is attained and k is the Boltzmann constant. Similarly, entropy in information theorymeasures the quantity of information. If a message recipient may expect any one of N possible messages with equal likelihood, then the amount of information conveyed by any one such message is quantified as log₂(N) bits.^[84]

Lyapunov exponents use logarithms to gauge the degree of chaoticity of a dynamical system. For example, for a particle moving on an oval billiard table, even small changes of the initial conditions result in very different paths of the particle. Such systems are chaotic in a deterministic way, because small measurement errors of the initial state predictably lead to largely different final states.^[85] At least one Lyapunov exponent of a deterministically chaotic system is positive.

[edit]Fractals

The Sierpinski triangle (at the right) is constructed by repeatedly replacingequilateral triangles by three smaller ones.

Logarithms occur in definitions of the dimension of fractals.^[86] Fractals are geometric objects that are self-similar: small parts reproduce, at least roughly, the entire global structure. TheSierpinski triangle (pictured) can be covered by three copies of itself, each having sides half the original length. This makes the Hausdorff dimension of this structure log(3)/log(2) ≈ 1.58. Another logarithm-based notion of dimension is obtained by counting the number of boxes needed to cover the fractal in question.

[edit]Music

Four different octaves shown on a linear scale, then shown on a logarithmic scale (as the ear hears them).

Logarithms are related to musical tones and intervals. In equal temperament, the frequency ratio depends only on the interval between two tones, not on the specific frequency, or pitch, of the individual tones. For example, the note A has a frequency of 440 Hz and B-flat has a frequency of 466 Hz. The interval between A and B-flat is a semitone, as is the one between B-flat and B (frequency 493 Hz). Accordingly, the frequency ratios agree:

$\frac{466}{440} \approx \frac{493}{466} \approx 1.059 \approx \sqrt[12]2.$

Therefore, logarithms can be used to describe the intervals: an interval is measured in semitones by taking the base-2^1/12 logarithm of the frequency ratio, while the base-2^1/1200 logarithm of the frequency ratio expresses the interval in cents, hundredths of a semitone. The latter is used for finer encoding, as it is needed for non-equal temperaments.^[87]

Interval (the two tones are played at the same time)	1/12 tone play (help·info)	Semitone play	Just major third play	Major third play	Tritone play	Octave play
Frequency ratio r	$2^{\frac 1 {72}} \approx 1.0097$	$2^{\frac 1 {12}} \approx 1.0595$	$\tfrac 5 4 = 1.25$	$\begin{align} 2^{\frac 4 {12}} & = \sqrt[3] 2 \\ & \approx 1.2599 \end{align}$	$\begin{align} 2^{\frac 6 {12}} & = \sqrt 2 \\ & \approx 1.4142 \end{align}$	$2^{\frac {12} {12}} = 2$
Corresponding number of semitones $\log_{\sqrt[12] 2}(r) = 12 \log_2 (r)$	$\tfrac 1 6 \,$	$1 \,$	$\approx 3.8631 \,$	$4 \,$	$6 \,$	$12 \,$
Corresponding number of cents $\log_{\sqrt[1200] 2}(r) = 1200 \log_2 (r)$	$16 \tfrac 2 3 \,$	$100 \,$	$\approx 386.31 \,$	$400 \,$	$600 \,$	$1200 \,$

[edit]Number theory

Natural logarithms are closely linked to counting prime numbers (2, 3, 5, 7, 11, ...), an important topic in number theory. For any integer x, the quantity of prime numbersless than or equal to x is denoted π(x). The prime number theorem asserts that π(x) is approximately given by

$\frac{x}{\ln(x)},$

in the sense that the ratio of π(x) and that fraction approaches 1 when x tends to infinity.^[88] As a consequence, the probability that a randomly chosen number between 1 and x is prime is inversely proportional to the numbers of decimal digits of x. A far better estimate of π(x) is given by the offset logarithmic integral function Li(x), defined by

$\mathrm{Li}(x) = \int_2^x \frac1{\ln(t)} \,dt.$

The Riemann hypothesis, one of the oldest open mathematical conjectures, can be stated in terms of comparing π(x) and Li(x).^[89] The Erdős–Kac theorem describing the number of distinct prime factors also involves the natural logarithm.

The logarithm of n factorial, n! = 1 · 2 · ... · n, is given by

$\ln (n!) = \ln (1) + \ln (2) + \cdots + \ln (n). \,$

This can be used to obtain Stirling's formula, an approximation of n! for large n.^[90]

[edit]Generalizations

[edit]Complex logarithm

Main article: Complex logarithm

Polar form of z = x + iy. Both φ and φ' are arguments of z.

The complex numbers a solving the equation

$e^a=z.\,$

are called complex logarithms. Here, z is a complex number. A complex number is commonly represented as z = x + iy, wherex and y are real numbers and i is the imaginary unit. Such a number can be visualized by a point in the complex plane, as shown at the right. The polar form encodes a non-zero complex number z by its absolute value, that is, the distance r to theorigin, and an angle between the x axis and the line passing through the origin and z. This angle is called the argument of z. The absolute value r of z is

$r=\sqrt{x^2+y^2}. \,$

The argument is not uniquely specified by z: both φ and φ' = φ + 2π are arguments of z because adding 2π radians or 360 degrees^{[nb 7]} to φ corresponds to "winding" around the origin counter-clock-wise by a turn. The resulting complex number is again z, as illustrated at the right. However, exactly one argument φ satisfies −π < φ and φ ≤ π. It is called the principal argument, denoted Arg(z), with a capital A.^[91] (An alternative normalization is 0 ≤ Arg(z) < 2π.^[92])

The principal branch of the complex logarithm, Log(z). The black point at z = 1corresponds to absolute value zero and brighter (more saturated) colors refer to bigger absolute values. The hue of the color encodes the argument of Log(z).

Using trigonometric functions sine and cosine, or the complex exponential, respectively, r and φ are such that the following identities hold:^[93]

$\begin{array}{lll}z& = & r \left (\cos \varphi + i \sin \varphi\right) \\ & = & r e^{i \varphi}. \end{array} \,$

This implies that the a-th power of e equals z, where

$a = \ln (r) + i ( \varphi + 2 n \pi ), \,$

φ is the principal argument Arg(z) and n is an arbitrary integer. Any such a is called a complex logarithm of z. There are infinitely many of them, in contrast to the uniquely defined real logarithm. If n = 0, a is called the principal value of the logarithm, denoted Log(z). The principal argument of any positive real number x is 0; hence Log(x) is a real number and equals the real (natural) logarithm. However, the above formulas for logarithms of products and powers do not generalize to the principal value of the complex logarithm.^[94]

The illustration at the right depicts Log(z). The discontinuity, that is, the jump in the hue at the negative part of the x- or real axis, is caused by the jump of the principal argument there. This locus is called a branch cut. This behavior can only be circumvented by dropping the range restriction on φ. Then the argument of z and, consequently, its logarithm become multi-valued functions.

[edit]Inverses of other exponential functions

Exponentiation occurs in many areas of mathematics and its inverse function is often referred to as the logarithm. For example, the logarithm of a matrix is the (multi-valued) inverse function of the matrix exponential.^[95] Another example is the p-adic logarithm, the inverse function of the p-adic exponential. Both are defined via Taylor series analogous to the real case.^[96] In the context of differential geometry, the exponential map maps the tangent space at a point of a manifold to a neighborhood of that point. Its inverse is also called the logarithmic (or log) map.^[97]

In the context of finite groups exponentiation is given by repeatedly multiplying one group element b with itself. The discrete logarithm is the integer n solving the equation

$b^n = x,\,$

where x is an element of the group. Carrying out the exponentiation can be done efficiently, but the discrete logarithm is believed to be very hard to calculate in some groups. This asymmetry has important applications in public key cryptography, such as for example in the Diffie–Hellman key exchange, a routine that allows secure exchanges of cryptographic keys over unsecured information channels.^[98] Zech's logarithm is related to the discrete logarithm in the multiplicative group of non-zero elements of a finite field.^[99]

Further logarithm-like inverse functions include the double logarithm ln(ln(x)), the super- or hyper-4-logarithm (a slight variation of which is called iterated logarithm in computer science), the Lambert W function, and the logit. They are the inverse functions of the double exponential function, tetration, of f(w) = we^w,^[100] and of the logistic function, respectively.^[101]

[edit]Related concepts

From the perspective of pure mathematics, the identity log(cd) = log(c) + log(d) expresses a group isomorphism between positive reals under multiplication and reals under addition. Logarithmic functions are the only continuous isomorphisms between these groups.^[102] By means of that isomorphism, the Haar measure (Lebesgue measure)dx on the reals corresponds to the Haar measure dx/x on the positive reals.^[103] In complex analysis and algebraic geometry, differential forms of the form df/f are known as forms with logarithmic poles.^[104]

The polylogarithm is the function defined by

$\operatorname{Li}_s(z) = \sum_{k=1}^\infty {z^k \over k^s}.$

It is related to the natural logarithm by Li₁(z) = −ln(1 − z). Moreover, Li_s(1) equals the Riemann zeta function ζ(s).^[105]

[edit]See also

· Index of logarithm articles

· Exponential function

[edit]Notes

1. ^ For further details, including the formula b^m⁺ⁿ = b^m · bⁿ, see exponentiation or^[1] for an elementary treatise.

2. ^ The restrictions on x and b are explained in the section "Analytic properties".

3. ^ Some mathematicians disapprove of this notation. In his 1985 autobiography,Paul Halmos criticized what he considered the "childish ln notation," which he said no mathematician had ever used.^[10] The notation was invented by Irving Stringham, a mathematician.^[11][12]

4. ^ For example C, Java, Haskell, and BASIC.

5. ^ The same series holds for the principal value of the complex logarithm for complex numbers z satisfying |z − 1| < 1.

6. ^ The same series holds for the principal value of the complex logarithm for complex numbers z with positive real part.

7. ^ See radian for the conversion between 2π and 360 degrees.

[edit]References

1. ^ Shirali, Shailesh (2002), A Primer on Logarithms, Hyderabad: Universities Press, ISBN 978-81-7371-414-6, esp. section 2

2. ^ Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8, chapter 1

3. ^ All statements in this section can be found in Shailesh Shirali 2002section 4, (Douglas Downing ,2003p. 275), or Kate , & Bhapkar 2009p. 1-1, for example. ,

4. ^ Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-005023-5, p. 21

5. ^ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, N.Y.: Barron's, ISBN 978-0-7641-1972-9, chapter 17, p. 275

6. ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, p. 20

7. ^ Franz Embacher; Petra Oberhuemer (in German), Mathematisches Lexikon, mathe online: für Schule, Fachhochschule, Universität unde Selbststudium, retrieved 22/03/2011

8. ^ B. N. Taylor (1995), Guide for the Use of the International System of Units (SI), US Department of Commerce

9. ^ Gullberg, Jan (1997), Mathematics: from the birth of numbers., New York: W. W. Norton & Co, ISBN 978-0-393-04002-9

10. ^ Paul Halmos (1985), I Want to Be a Mathematician: An Automathography, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96078-4

11. ^ Irving Stringham (1893), Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis, The Berkeley Press, p. xiii

12. ^ Roy S. Freedman (2006), Introduction to Financial Technology, Amsterdam: Academic Press, p. 59, ISBN 978-0-12-370478-8

13. ^ McFarland, David (2007), Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and Later Implementations in Analog Computers, p. 1

14. ^ Robson, Eleanor (2008). Mathematics in Ancient Iraq: A Social History. p. 227.ISBN 978-0691091822.

15. ^ Stifelio, Michaele (1544), Arithmetica Integra, London: Iohan Petreium

16. ^ Bukhshtab, A.A.; Pechaev, V.I. (2001), "Arithmetic", in Hazewinkel, Michiel,Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

17. ^ Vivian Shaw Groza and Susanne M. Shelley (1972), Precalculus mathematics, New York: Holt, Rinehart and Winston, p. 182, ISBN 978-0-03-077670-0

18. ^ Ernest William Hobson (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press

19. ^ Boyer 1991Chapter 14, section "Jobst Bürgi" ,

20. ^ Gladstone-Millar, Lynne (2003), John Napier: Logarithm John, National Museums Of Scotland, ISBN 978-1-901663-70-9, p. 44

21. ^ Napier, Mark (1834), Memoirs of John Napier of Merchiston, Edinburgh: William Blackwood, p. 392.

22. ^ William Harrison De Puy (1893), The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint,, 17 (9th ed.), Werner Co., p. 179

23. ^ Maor, Eli (2009), e: The Story of a Number, Princeton University Press, ISBN 978-0-691-14134-3, section 2

24. ^ J. J. O'Connor; E. F. Robertson (2001-09), The number e, The MacTutor History of Mathematics archive, retrieved 02/02/2009

25. ^ Cajori, Florian (1991), A History of Mathematics (5th ed.), Providence, RI: AMS Bookstore, ISBN 978-0-8218-2102-2, p. 152

26. ^ ^a ^b Maor 2009sections 1, 13 ,

27. ^ Eves, Howard Whitley (1992), An introduction to the history of mathematics, The Saunders series (6th ed.), Philadelphia: Saunders, ISBN 978-0-03-029558-4, section 9-3

28. ^ Boyer, Carl B. (1991), A History of Mathematics, New York: John Wiley & Sons,ISBN 978-0-471-54397-8, p. 484, 489

29. ^ Bryant, Walter W., A History of Astronomy, London: Methuen & Co, p. 44

30. ^ Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, Oxford scholarship online, Oxford University Press, ISBN 978-0-19-850841-0, section 2

31. ^ Abramowitz, Milton; Stegun, Irene A., eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (10th ed.), New York:Dover Publications, ISBN 978-0-486-61272-0, section 4.7., p. 89

32. ^ Spiegel, Murray R.; Moyer, R.E. (2006), Schaum's outline of college algebra, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-145227-4, p. 264

33. ^ Devlin, Keith (2004). Sets, functions, and logic: an introduction to abstract mathematics. Chapman & Hall/CRC mathematics (3rd ed.). Boca Raton, Fla: Chapman & Hall/CRC. ISBN 978-1-58488-449-1.^{[verification
needed]}, or see the references in function

34. ^ ^a ^b Lang, Serge (1997), Undergraduate analysis, Undergraduate Texts in Mathematics (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94841-6, MR 1476913, section III.3

35. ^ ^a ^b Lang 1997section IV.2 ,

36. ^ Stewart, James (2007), Single Variable Calculus: Early Transcendentals, Belmont: Thomson Brooks/Cole, ISBN 978-0-495-01169-9, section 1.6

37. ^ "Calculation of d/dx(Log(b,x))". Wolfram Alpha. Wolfram Research. Retrieved 15 March 2011.

38. ^ Kline, Morris (1998), Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications, ISBN 978-0-486-40453-0, p. 386

39. ^ "Calculation of Integrate(ln(x))". Wolfram Alpha. Wolfram Research. Retrieved 15 March 2011.

40. ^ Abramowitz & Stegun, eds. 1972p. 69 ,

41. ^ Courant, Richard (1988), Differential and integral calculus. Vol. I, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-60842-4, MR 1009558, section III.6

42. ^ Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5, sections 11.5 and 13.8

43. ^ Nomizu, Katsumi (1996), Selected papers on number theory and algebraic geometry, 172, Providence, RI: AMS Bookstore, p. 21, ISBN 978-0-8218-0445-2

44. ^ Baker, Alan (1975), Transcendental number theory, Cambridge University Press,ISBN 978-0-521-20461-3, p. 10

45. ^ Muller, Jean-Michel (2006), Elementary functions (2nd ed.), Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-4372-0, sections 4.2.2 (p. 72) and 5.5.2 (p. 95)

46. ^ Hart, Cheney, Lawson et al. (1968), Computer Approximations, SIAM Series in Applied Mathematics, New York: John Wiley, section 6.3, p. 105–111

47. ^ Zhang, M.; Delgado-Frias, J.G.; Vassiliadis, S. (1994), "Table driven Newton scheme for high precision logarithm generation", IEE Proceedings Computers & Digital Techniques 141 (5): 281–292, doi:10.1049/ip-cdt:19941268,ISSN 1350-387, section 1 for an overview

48. ^ Meggitt, J. E. (April 1962), "Pseudo Division and Pseudo Multiplication Processes", IBM Journal, doi:10.1147/rd.62.0210

49. ^ Kahan, W. (May 20, 2001), Pseudo-Division Algorithms for Floating-Point Logarithms and Exponentials

50. ^ ^a ^b Abramowitz & Stegun, eds. 1972p. 68 ,

51. ^ Sasaki, T.; Kanada, Y. (1982), "Practically fast multiple-precision evaluation of log(x)", Journal of Information Processing 5 (4): 247–250, retrieved 30 March 2011

52. ^ Ahrendt, Timm (1999), Fast computations of the exponential function, Lecture notes in computer science, 1564, Berlin, New York: Springer, pp. 302–312,doi:10.1007/3-540-49116-3_28

53. ^ Maor 2009p. 135 ,

54. ^ Frey, Bruce (2006), Statistics hacks, Hacks Series, Sebastopol, CA: O'Reilly,ISBN 978-0-596-10164-0, chapter 6, section 64

55. ^ Ricciardi, Luigi M. (1990), Lectures in applied mathematics and informatics, Manchester: Manchester University Press, ISBN 978-0-7190-2671-3, p. 21, section 1.3.2

56. ^ Bakshi, U. A. (2009), Telecommunication Engineering, Pune: Technical Publications, ISBN 978-81-8431-725-1, section 5.2

57. ^ Maling, George C. (2007), "Noise", in Rossing, Thomas D., Springer handbook of acoustics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-30446-5, section 23.0.2

58. ^ Tashev, Ivan Jelev (2009), Sound Capture and Processing: Practical Approaches, New York: John Wiley & Sons, ISBN 978-0-470-31983-3, p. 48

59. ^ Chui, C.K. (1997), Wavelets: a mathematical tool for signal processing, SIAM monographs on mathematical modeling and computation, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-384-8, p. 180

60. ^ Crauder, Bruce; Evans, Benny; Noell, Alan (2008), Functions and Change: A Modeling Approach to College Algebra (4th ed.), Boston: Cengage Learning,ISBN 978-0-547-15669-9, section 4.4.

61. ^ Bradt, Hale (2004), Astronomy methods: a physical approach to astronomical observations, Cambridge Planetary Science, Cambridge University Press,ISBN 978-0-521-53551-9, section 8.3, p. 231

62. ^ IUPAC (1997), A. D. McNaught, A. Wilkinson, ed., Compendium of Chemical Terminology ("Gold Book") (2nd ed.), Oxford: Blackwell Scientific Publications,doi:10.1351/goldbook, ISBN 978-0-9678550-9-7

63. ^ Bird, J. O. (2001), Newnes engineering mathematics pocket book (3rd ed.), Oxford: Newnes, ISBN 978-0-7506-4992-6, section 34

64. ^ Goldstein, E. Bruce (2009), Encyclopedia of Perception, Encyclopedia of Perception, Thousand Oaks, CA: Sage, ISBN 978-1-4129-4081-8, p. 355–356

65. ^ Matthews, Gerald (2000), Human performance: cognition, stress, and individual differences, Human Performance: Cognition, Stress, and Individual Differences, Hove: Psychology Press, ISBN 978-0-415-04406-6, p. 48

66. ^ Welford, A. T. (1968), Fundamentals of skill, London: Methuen, ISBN 978-0-416-03000-6, OCLC 219156, p. 61

67. ^ Paul M. Fitts (June 1954), "The information capacity of the human motor system in controlling the amplitude of movement", Journal of Experimental Psychology 47(6): 381–391, doi:10.1037/h0055392, PMID 13174710, reprinted in Paul M. Fitts (1992), "The information capacity of the human motor system in controlling the amplitude of movement" (PDF), Journal of Experimental Psychology: General121 (3): 262–269, doi:10.1037/0096-3445.121.3.262, PMID 1402698, retrieved 30 March 2011

68. ^ Banerjee, J. C. (1994), Encyclopaedic dictionary of psychological terms, New Delhi: M.D. Publications, ISBN 978-81-85880-28-0, OCLC 33860167, p. 304

69. ^ Nadel, Lynn (2005), Encyclopedia of cognitive science, New York: John Wiley & Sons, ISBN 978-0-470-01619-0, lemmas Psychophysics and Perception: Overview

70. ^ Siegler, Robert S.; Opfer, John E. (2003), "The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity",Psychological Science 14 (3): 237–43, doi:10.1111/1467-9280.02438,PMID 12741747

71. ^ Dehaene, Stanislas; Izard, Véronique; Spelke, Elizabeth; Pica, Pierre (2008), "Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures", Science 320 (5880): 1217–1220,doi:10.1126/science.1156540, PMC 2610411, PMID 18511690

72. ^ Breiman, Leo (1992), Probability, Classics in applied mathematics, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-296-4, section 12.9

73. ^ Aitchison, J.; Brown, J. A. C. (1969), The lognormal distribution, Cambridge University Press, ISBN 978-0-521-04011-2, OCLC 301100935

74. ^ Jean Mathieu and Julian Scott (2000), An introduction to turbulent flow, Cambridge University Press, p. 50, ISBN 978-0-521-77538-0

75. ^ Rose, Colin; Smith, Murray D. (2002), Mathematical statistics with Mathematica, Springer texts in statistics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-95234-5, section 11.3

76. ^ Tabachnikov, Serge (2005), Geometry and Billiards, Providence, R.I.: American Mathematical Society, pp. 36–40, ISBN 978-0-8218-3919-5, section 2.1

77. ^ Durtschi, Cindy; Hillison, William; Pacini, Carl (2004), "The Effective Use of Benford's Law in Detecting Fraud in Accounting Data", Journal of Forensic Accounting V: 17–34

78. ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, pages 1-2

79. ^ Harel, David; Feldman, Yishai A. (2004), Algorithmics: the spirit of computing, New York: Addison-Wesley, ISBN 978-0-321-11784-7, p. 143

80. ^ Knuth, Donald (1998), The Art of Computer Programming, Reading, Mass.: Addison-Wesley, ISBN 978-0-201-89685-5, section 6.2.1, pp. 409–426

81. ^ Donald Knuth 1998section 5.2.4, pp. 158–168 ,

82. ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, p. 20, ISBN 978-3-540-21045-0

83. ^ Mohr, Hans; Schopfer, Peter (1995), Plant physiology, Berlin, New York: Springer-Verlag, ISBN 978-3-540-58016-4, chapter 19, p. 298

84. ^ Eco, Umberto (1989), The open work, Harvard University Press, ISBN 978-0-674-63976-8, section III.I

85. ^ Sprott, Julien Clinton (2010), Elegant Chaos: Algebraically Simple Chaotic Flows, New Jersey: World Scientific, ISBN 978-981-283-881-0, section 1.9

86. ^ Helmberg, Gilbert (2007), Getting acquainted with fractals, De Gruyter Textbook, Berlin, New York: Walter de Gruyter, ISBN 978-3-11-019092-2

87. ^ Wright, David (2009), Mathematics and music, Providence, RI: AMS Bookstore,ISBN 978-0-8218-4873-9, chapter 5

88. ^ Bateman, P. T.; Diamond, Harold G. (2004), Analytic number theory: an introductory course, New Jersey: World Scientific, ISBN 978-981-256-080-3,OCLC 492669517, theorem 4.1

89. ^ P. T. Bateman & Diamond 2004Theorem 8.15 ,

90. ^ Slomson, Alan B. (1991), An introduction to combinatorics, London: CRC Press,ISBN 978-0-412-35370-3, chapter 4

91. ^ Ganguly, S. (2005), Elements of Complex Analysis, Kolkata: Academic Publishers, ISBN 978-81-87504-86-3, Definition 1.6.3

92. ^ Nevanlinna, Rolf Herman; Paatero, Veikko (2007), Introduction to complex analysis, Providence, RI: AMS Bookstore, ISBN 978-0-8218-4399-4, section 5.9

93. ^ Moore, Theral Orvis; Hadlock, Edwin H. (1991), Complex analysis, Singapore:World Scientific, ISBN 978-981-02-0246-0, section 1.2

94. ^ Wilde, Ivan Francis (2006), Lecture notes on complex analysis, London: Imperial College Press, ISBN 978-1-86094-642-4, theorem 6.1.

95. ^ Higham, Nicholas (2008), Functions of Matrices. Theory and Computation, Philadelphia, PA: SIAM, ISBN 978-0-89871-646-7, chapter 11.

96. ^ Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, Zbl 0956.11021, MR 1697859, section II.5.

97. ^ Hancock, Edwin R.; Martin, Ralph R.; Sabin, Malcolm A. (2009), Mathematics of Surfaces XIII: 13th IMA International Conference York, UK, September 7–9, 2009 Proceedings, Springer, p. 379, ISBN 978-3-642-03595-1

98. ^ Stinson, Douglas Robert (2006), Cryptography: Theory and Practice (3rd ed.), London: CRC Press, ISBN 978-1-58488-508-5

99. ^ Lidl, Rudolf; Niederreiter, Harald (1997), Finite fields, Cambridge University Press, ISBN 978-0-521-39231-0

100. ^ Corless, R.; Gonnet, G.; Hare, D.; Jeffrey, D.; Knuth, Donald (1996), "On the Lambert W function", Advances in Computational Mathematics (Berlin, New York: Springer-Verlag) 5: 329–359, doi:10.1007/BF02124750, ISSN 1019-7168

101. ^ Cherkassky, Vladimir; Cherkassky, Vladimir S.; Mulier, Filip (2007), Learning from data: concepts, theory, and methods, Wiley series on adaptive and learning systems for signal processing, communications, and control, New York: John Wiley & Sons, ISBN 978-0-471-68182-3, p. 357

102. ^ Bourbaki, Nicolas (1998), General topology. Chapters 5—10, Elements of Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64563-4,MR 1726872, section V.4.1

103. ^ Ambartzumian, R. V. (1990), Factorization calculus and geometric probability,Cambridge University Press, ISBN 978-0-521-34535-4, section 1.4

104. ^ Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, DMV Seminar, 20, Basel, Boston: Birkhäuser Verlag, ISBN 978-3-7643-2822-1,MR 1193913, section 2

105. ^ Apostol, T.M. (2010), "Logarithm", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248