Théorème des résidus

Le théorème des résidus en analyse complexe est un outil puissant pour évaluer des intégrales curvilignes de fonctions holomorphes sur des courbes fermées ; il peut aussi bien être utilisé pour calculer des intégrales de fonctions réelles ainsi que la somme de certaines séries. Il généralise le théorème intégral de Cauchy et la formule intégrale de Cauchy.

Sommaire

[masquer]

· 1 Énoncé

· 2 Variante

· 3 Application au calcul d'intégrales réelles

· 4 Application aux calculs de sommes

o 4.1 Premier type

o 4.2 Second type

· 5 Voir aussi

· 6 Note et références

Énoncé[modifier]

Soient U un sous-ensemble ouvert et simplement connexe du plan complexe ℂ, z₁,...,z_n un ensemble de points distincts et isolés de U et f une fonction définie et holomorphe sur U\ {z₁,...,z_n}.

Si γ est une courbe rectifiable dans U qui ne rencontre aucun des points singuliers z_k et dont le point de départ correspond au point d'arrivée (c'est-à-dire un lacet rectifiable), alors :

$\oint_\gamma f(z)~\mathrm dz= 2\pi i \sum_{k=1}^n \operatorname{Res}( f, z_k )\,\mathrm{Ind}_\gamma(z_k).$

Ici, Res(f,z_k) désigne le résidu de f en z_k, et $\mathrm{Ind}_\gamma(z_k)$ l'indice du lacet γ par rapport à z_k. Intuitivement, l'indice du lacet est le nombre de tours autour de z_k effectués par un point parcourant tout le lacet. Ce nombre de tours est un entier ; il est positif si γ est parcouru dans le sens inverse des aiguilles d'une montre (sens direct) autour de z_k, nul si γ ne se déplace pas du tout autour de z_k, et négatif si γ est parcouru dans le sens des aiguilles d'une montre autour de z_k.

L'indice est défini par

$\operatorname{Ind}_\gamma(z_k) = \frac{1}{2\pi i} \int_{\gamma} \frac{\text{d}z}{z-z_k}.$

[afficher]

Démonstration

Variante[modifier]

« Soit D un ouvert de la sphère de Riemann S₂, et soit f une fonction holomorphe dans D sauf peut-être en des points isolés qui sont singuliers pour f. Soit Γ le bord orienté d'un compact A contenu dans D, et supposons que Γ ne contienne aucun point singulier de f, ni le point à l'infini. Les points singuliers z_k contenus dans A sont alors en nombre fini, et on a la relation :

$\int_\Gamma f(z)~\mathrm dz=2\pi i \sum_k \operatorname{Res}( f, z_k ),$

où Res(f, z_k) désigne le résidu de la fonction f au point z_k ; la sommation est étendue à tous les points singuliers z_k∈A, y compris éventuellement le point à l'infini¹. »

Application au calcul d'intégrales réelles[modifier]

Pour évaluer des intégrales réelles, le théorème des résidus s'utilise souvent de la façon suivante : l'intégrande est prolongé en une fonction holomorphe sur un ouvert du plan complexe ; ses résidus sont calculés, et une partie de l'axe réel est étendue à une courbe fermée en lui attachant un demi-cercle dans le demi-plan supérieur ou inférieur. L'intégrale suivant cette courbe peut alors être calculée en utilisant le théorème des résidus. Souvent, la partie de l'intégrale sur le demi-cercle tend vers zéro (lemme de Jordan), quand le rayon de ce dernier tend vers l'infini, laissant seulement la partie de l'intégrale sur l'axe réel, celle qui initialement nous intéressait.

La liste ci-dessous n'est pas exhaustive mais elle permet d'avoir une idée générale de la technique utilisant le théorème des résidus, on aborde :

§ Les intégrales du « premier type » : $\int_0^{2\pi}R(\cos(t),\sin(t))~\mathrm dt$ où $R$ est une fonction rationnelle,

§ Les intégrales du « second type » : $\int_{-\infty}^{+\infty}f(x)~\mathrm dx$ ,

§ Les intégrales du « troisième type » : $\int_{-\infty}^{+\infty}f(x)\mathrm e^{iax}~\mathrm dx$ ,

§ Les intégrales du « quatrième type » : combinaison des deux cas précédents en considérant la valeur principale de Cauchy de l'intégrale.

Premier type[modifier]

Soit le calcul de l'intégrale réelle suivante :

$I=\int_0^{2\pi}R(\cos(t),\sin(t))~\mathrm dt$

avec $R$ une fonction rationnelle ayant un nombre fini de points singuliers $z_j$ n'appartenant pas au cercle $C(0, 1)$ centré à l'origine et de rayon 1. On obtient par le théorème des résidus :

$I=2i\pi\sum_{|z_j|<1}\mathrm{Res}(f, z_j)$

où $f$ est définie comme suit :

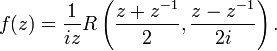
$f(z)=\frac1{iz}R\left(\frac{z+z^{-1}}2, \frac{z-z^{-1}}{2i}\right).$

[afficher]

Démonstration

[afficher]

Exemple

Second type[modifier]

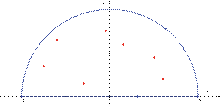
Figure 1. Illustration du contour $\gamma$ (en bleu) utilisé dans la démonstration des intégrales du second type. Les singularités (purement complexes) de $f$ appartenant au plan supérieur sont représentées en rouge.

Soit le calcul de l'intégrale réelle suivante :

$I=\int_{-\infty}^{+\infty}f(x)~\mathrm dx$

avec $f$ ayant un ensemble de points singuliers isolés $z_j$ purement complexes. S'il existe $M,R>0$ et $\alpha>1$ tels que $|f(z)|\le{M\over|z|^\alpha}$ pour tout complexe $z$ de module supérieur ou égal à $R$ , alors

$\int_{-\infty}^{+\infty}|f(x)|~\mathrm dx<+\infty$

$I=2i\pi\sum_{\Im(z_j)>0}\mathrm{Res}(f,z_j)=-2i\pi\sum_{\Im(z_j)<0}\mathrm{Res}(f, z_j).$

Remarque : dans le cas où $f$ est une fonction rationnelle définie par $f(z)={P(z)\over Q(z)}$ avec $P$ et $Q$ des polynômes, il suffit d'exiger que $\mathrm{deg}(Q)\ge\mathrm{deg}(P)+2$ (où $\mathrm{deg}$ représente le degré du polynôme) pour vérifier les hypothèses et appliquer l'identité.

[afficher]

Démonstration

[afficher]

Exemple

Troisième type[modifier]

Figure 2. Illustration du contour $\gamma$ (en bleu) utilisé dans la démonstration des intégrales du troisième type. Les points singuliers (purement complexes) de $f$ appartenant au demi-plan supérieur sont représentés en rouge.

Soit le calcul de l'intégrale réelle suivante :

$I=\int_{-\infty}^{+\infty}f(x)\mathrm e^{iax}~\mathrm dx$

avec $f$ comportant un ensemble de point singuliers isolés purement complexes. S'il existe $M,R>0$ tels que $|f(z)|\le\frac M{|z|}$ pour tout complexe $z$ de module supérieur ou égal à $R$ , alors :

$(\mathrm{si}\,\,a>0),\quad I=2i\pi\sum_{\Im(z_j)>0}\mathrm{Res}\left(f(z)\mathrm e^{iaz},z_j\right)$

$(\mathrm{si}\,\,a<0),\quad I=-2i\pi\sum_{\Im(z_j)<0}\mathrm{Res}\left(f(z)\mathrm e^{iaz},z_j\right).$

[afficher]

Démonstration

[afficher]

Exemple

Quatrième type[modifier]

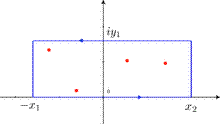
Figure 3. Illustration du contour $\gamma$ (en bleu) utilisé dans la démonstration des intégrales du quatrième type. Les singularités (purement complexes) de $f$ appartenant au plan supérieur sont représentées en rouge. En vert ce sont les pôles simples réels.

Les intégrales du second et du troisième type s'étendent aux cas avec un nombre fini n de pôles situés sur l'axe réel. Il s'agit alors d'une intégrale impropre et l'on considère alors la valeur principale de Cauchy de l'intégrale.

Soit $f$ une fonction holomorphe sur ℂ sauf en un ensemble de pôles simples réels, $x_j$ , et de singularités isolées purement complexes, $z_j$ . Supposons que l'on se trouve dans un des deux cas suivant :

§ il existe $M,R>0$ et $\alpha>1$ tels que $|f(z)|\le{M\over|z|^\alpha}$ pour tout complexe $z$ de module supérieur ou égal à $R$ ,

§ $f(z)=g(z)\mathrm e^{iaz}$ avec $a>0$ et il existe $M,R>0$ tels que $|g(z)|\le{M\over|z|}$ pour tout complexe $z$ de module supérieur ou égal à $R$ .

Alors la valeur principale de Cauchy (notée $\mathrm{v.p.}$ ) de l'intégrale existe et on a :

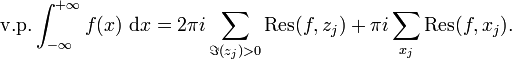
$\mathrm{v.p.}\int_{-\infty}^{+\infty}f(x)~\mathrm dx=2\pi i\sum_{\Im(z_j)>0}\mathrm{Res}(f,z_j)+\pi i\sum_{x_j}\mathrm{Res}(f,x_j).$

Remarque : on peut aisément étendre la formule au demi-plan inférieur en changeant le signe de la première somme et en considérant uniquement les singularités purement complexe dans ce demi-plan.

[afficher]

Démonstration

[afficher]

Exemple

Application aux calculs de sommes[modifier]

Le théorème des résidus permet aussi de calculer certaines sommes infinies. Soit une fonction $g$ ayant pour chaque entier $n$ un résidu égal au $n$ -ième terme général d'une somme infinie $S$ ainsi qu'un ensemble $E$ de résidus correspondant à d'autres points. Supposons que l'intégrale de cette fonction le long d'un lacet $\gamma$ rectifiable infiniment grand soit nulle. On a alors par le théorème des résidus :

$\int_\gamma g(z)~\mathrm dz=2i\pi\left[S+\sum_{z_k\in E}\mathrm{Res}(g;z_k)\right]=0.$

Par conséquent, on peut exprimer la somme infinie par une autre somme (en général finie) de résidus :

$S=-\sum_{z_k\in E}\mathrm{Res}(g;z_k).$

Les énoncés ci-dessous donnent des exemples plus généraux de cas pour lesquels cette méthode est applicable :

§ les sommes du "premier type" : $\sum f(n)$ ;

§ les sommes du "second type" : $\sum (-1)^nf(n)$ .

Premier type[modifier]

Soit le calcul de la somme suivante :

$S=\sum_{-\infty,n\notin E}^\infty f(n)$

avec $f$ ayant un ensemble $E$ de singularités isolées. Supposons que la condition suivante soit respectée :

il existe $M,R>0$ et $\alpha>1$ tels que $|f(z)|\le{M\over |z|^\alpha}$ pour tout complexe $z$ de module supérieur ou égal à $R$ .

Alors, nous avons :

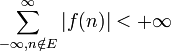
$\sum_{-\infty,n\notin E}^\infty|f(n)|<+\infty$

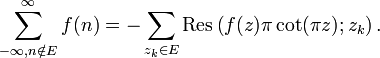
$\sum_{-\infty,n\notin E}^\infty f(n)=-\sum_{z_k\in E}\mathrm{Res}\left(f(z)\pi\cot(\pi z);z_k\right).$

[afficher]

Démonstration

[afficher]

Exemple

Second type[modifier]

Soit le calcul de la somme suivante :

$S=\sum_{-\infty,n\notin E}^\infty(-1)^nf(n)$

avec $f$ ayant un ensemble $E$ de singularités isolées. Supposons que $f$ satisfasse à la même condition que pour les sommes du premier type à savoir :

il existe $M,R>0,\alpha>1$ tels que $|f(z)|\le{M\over|z|^\alpha}$ pour tout pour tout complexe $z$ de module supérieur ou égal à $R$ .

Alors, la somme converge absolument et on a :

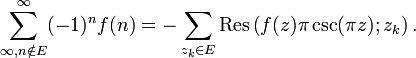
$\sum_{\infty,n\notin E}^\infty(-1)^nf(n)=-\sum_{z_k\in E}\mathrm{Res}\left(f(z)\pi\csc(\pi z);z_k\right).$

[afficher]

Démonstration

[afficher]

Exemple

Voir aussi[modifier]

§ Fonction multivaluée

§ Principe de l'argument

§ Lemme de Jordan

§ Intégrale de contour (en)

§ Contour de Hankel (en)

Note et références[modifier]

1. ↑ Henri Cartan, Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes [détail des éditions], p. 93

§ Murray R. Spiegel (en), Variables Complexes, Schaum (ISBN 2-7042-0020-3)

§ (en) Serge Lang, Complex Analysis, 4^e éd., Springer, 1999 (ISBN 0-387-98592-1)

§ (en) Joseph Bak et Donald J. Newman (en), Complex Analysis, 2^e éd., Springer, 1997 (ISBN 0-387-94756-6)

§ Ernst Lindelöf, Le calcul des résidus et ses applications à la théorie des fonctions, Gauthier-Villars, Paris, 1905