Transformée de Laplace

Pour les articles homonymes, voir Laplace.

En mathématiques, la transformation de Laplace est une transformation intégrale, c'est-à-dire une opération associant à une fonction (à valeur dans $\mathbb{R}^{n}$ ou dans $\mathbb{C}^{n}$ ) $f\left(t\right)$ une nouvelle fonction dite transformée de $f\left(t\right)$ , notée traditionnellement $F\left(p\right)$ , via une intégrale. La transformation de Laplace est bijective et par usage de tables il est possible d'inverser la transformation. Le grand avantage de la transformation de Laplace est que la plupart des opérations courantes sur la fonction originale $f\left(t\right)$ , telle que la dérivation, ou un décalage sur la variable t, ont une traduction (plus) simple sur la transformée $F\left(p\right)$ . Ainsi la transformée de Laplace de la dérivée $f^\prime\left(t\right)$ est simplement $pF\left(p\right) - f(0^{-})$ , et la transformée de la fonction « décalée » $f\left(t - \tau\right)$ est simplement $e^{-p\tau} F\left(p\right)$ . Cette transformation fut introduite pour la première fois sur une forme proche de celle utilisée par Laplace en 1774, dans le cadre de la théorie des probabilités

La transformée de Laplace est proche de la transformée de Fourier qui est également utilisée pour résoudre les équations différentielles, mais contrairement à cette dernière elle tient compte des conditions initiales et peut ainsi être utilisée en théorie des vibrations mécaniques ou en électricité dans l'étude des régimes forcés sans négliger le régime transitoire. Dans ce type d'analyse, la transformée de Laplace est souvent interprétée comme un passage du domaine temps, dans lequel les entrées et sorties sont des fonctions du temps, dans le domaine des fréquences, dans lequel les mêmes entrées et sorties sont des fonctions de la « fréquence » (complexe) p. Ainsi il est possible d'analyser simplement l'effet du système sur l'entrée pour donner la sortie en terme d'opérations algébriques simples (cf. théorie des fonctions de transfert en électronique ou en mécanique).

Sommaire

[masquer]

· 2 Inversion

o 3.3 Application à la dérivée de la fonction de Heaviside

o 3.4 Multiplication par une puissance de t

o 3.5 Intégration

o 3.6 Valeur finale

o 3.7 Valeur initiale

o 3.8 Convolution

o 3.9 Transformée de Laplace d'une fonction de période T

o 3.10 Tableau résumé des propriétés de la transformée de Laplace

· 4 Quelques transformées usuelles

· 5 Exemple d'utilisation de la transformée de Laplace en électricité

o 5.1 Charge d'un condensateur par un échelon de tension

· 6 Notes et références

o 6.1 Notes

o 6.2 Références

· 7 Voir aussi

o 7.1 Articles connexes

o 7.2 Lien externe

Définition[modifier]

En mathématiques et en particulier en analyse fonctionnelle, la transformée de Laplace monolatérale d'une fonction $f$ (éventuellement généralisée, telle que la « fonction de Dirac ») d'une variable réelle t, à support positif, est la fonction $F$ de la variable complexe p, définie par:

$F(p) = \mathcal{L}\{f(t)\} =\int_{0^{-}}^{+\infty } e^{-pt} f(t)\,dt.$

Plus précisément, cette formule est valide lorsque (1) $\Re \left( p\right)> \alpha$ où $\alpha , -\infty \leq \alpha \leq +\infty ,$ est l'abscisse de convergence (définie plus bas), et (2) $f$ est un « germe (en) » $f$ de distributions définies dans un voisinage ouvert (et borné inférieurement) de l'intervalle $I = \left[ 0,+\infty \right[$ dont la restriction au complémentaire de $I$ dans ce voisinage est une fonction indéfiniment dérivable (voir l'article Transformée bilatérale de Laplace)¹. C'est un tel germe que nous appelons ici, par abus de langage, une fonction généralisée à support positif, et la transformation de Laplace est injective appliquée à ces fonctions généralisées. L'abscisse de convergence $\alpha$ se définit comme suit: soit, pour un réel $\beta$ , $f_{\beta }:t\mapsto e^{-\beta t}f\left( t\right)$ . Alors $\alpha$ est la borne inférieure de l'ensemble $B$ des $\beta$ pour lesquels $f_{\beta }$ est une distribution tempérée si $B$ est non vide, et $\alpha = +\infty$ sinon.

La « fonction de Dirac » est de cette nature. Sa transformée de Laplace vaut 1 avec une abscisse de convergence de $-\infty$ .

Les propriétés de cette transformation lui confèrent une grande utilité dans l'analyse des systèmes dynamiques linéaires. La plus intéressante de ces propriétés est que l'intégration et la dérivation sont transformées en division et multiplication par p, de la même manière que le logarithme transforme la multiplication en addition. Elle permet ainsi de ramener la résolution des équations différentielles linéaires à coefficients constants à la résolution d'équations affines (dont les solutions sont des fonctions rationnelles de p) (voir Application de la transformation de Laplace aux équations différentielles).

La transformation de Laplace est très utilisée par les ingénieurs pour résoudre des équations différentielles et déterminer la fonction de transfert d'un système linéaire. Par exemple, en électronique, contrairement à la décomposition de Fourier qui est utilisée pour la détermination du spectre d'un signal périodique ou même quelconque, elle tient compte de l'existence d'un régime transitoire précédant le régime permanent (exemple : la prise en compte de l'allure du signal avant et après la mise en marche d'un générateur de fréquence).

Il suffit en effet de transposer l'équation différentielle dans le domaine de Laplace pour obtenir une équation beaucoup plus simple à manipuler.

Par exemple, lors de l'étude d'une machine à courant continu : $e(t)=R \cdot i(t)+L\, \frac{di(t)}{dt}\,$ dans le domaine temporel devient $E(p)=R \cdot I(p)+p \cdot L \cdot I(p)\,$ dans le domaine de Laplace. Ceci n'est valable qu'à conditions initiales nulles ( $i(0) = 0)$ .

On a utilisé ici des propriétés de la transformation de Laplace, explicitées ci-dessous.

Remarque : la notation « s » (variable de Laplace) est souvent utilisée dans les pays anglo-saxons alors que la notation « p » est utilisée notamment en France et en Allemagne.

On définit aussi, dans les mêmes conditions que ci-dessus, la transformation de Laplace-Carson par²:

$\phi(p)=p\int_{0^{-}}^{+\infty} e^{-pt} f(t)\,dt$ qui permet d'associer à toute fonction d'une variable $t\mapsto f(t)$ une fonction image $p\mapsto \phi(p)$

Cette transformée est utilisée par certains ingénieurs car :

§ une constante sur $\left[ 0,+\infty \right[$ a pour image la même constante ;

§ elle offre dans certains cas une plus grande facilité d'emploi en calcul matriciel et tensoriel.

Inversion[modifier]

Article détaillé : Transformée inverse de Laplace.

L'inversion de la transformation de Laplace s'effectue par le biais d'une intégrale dans le plan complexe. À l'aide du théorème des résidus, on démontre la formule deBromwich (en)-Mellin:

$f(t) = \mathcal{L}^{-1} \{F(p)\} = \frac{1}{2 \pi i} \int_{ \gamma - i \cdot \infty}^{ \gamma + i \cdot \infty} e^{pt} F(p)\,dp,$

où $\gamma$ est choisi de sorte que l'intégrale soit convergente, ce qui implique que $\gamma$ soit supérieur à la partie réelle de toute singularité de $F(p)$ et qu'à l'infini, $\left\vert F(p) \right\vert$ tende vers $0$ au moins aussi rapidement que $\dfrac{1}{\left\vert p\right\vert ^{2}}$ . Lorsque cette dernière condition n'est pas satisfaite, la formule ci-dessus est encore utilisable s'il existe un entier $n$ tel que $\left\vert p^{-n} F(p) \right\vert$ tende vers $0$ aussi rapidement que $\dfrac{1}{\left\vert p\right\vert ^{2}}$ , c'est-à-dire lorsque, pour $\left\vert p\right\vert$ tendant vers l'infini, $\left\vert F\left( p\right) \right\vert$ est majorée par un polynôme en $\left\vert p\right\vert$ . En remplaçant $F(p)$ par $p^{-n} F(p)$ dans l'intégrale ci-dessus, on trouve dans le membre de gauche de l'égalité une fonction généralisée à support positif dont la dérivée d'ordre $n$ (au sens des distributions) est la fonction généralisée (elle aussi à support positif) cherchée.

En pratique néanmoins, la formule de Bromwich-Mellin est peu utilisée, et on calcule les inverses des transformées de Laplace à partir des tables de transformées de Laplace.

Propriétés[modifier]

Linéarité[modifier]

$\mathcal{L}\left\{a f + b g \right\} = a\, \mathcal{L}\left\{ f \right\} + b\, \mathcal{L}\left\{ g \right\}$

Dérivation[modifier]

Article détaillé : Dérivée.

Soit à calculer :

$\mathcal{L}\{f'\} = \int_{0^{-}}^{\infty} e^{-pt} f'(t)\,dt\,.$

En intégrant par parties, on obtient :

$\mathcal{L}\{f'\} = \left[e^{-pt}f(t)\right]_{0^{-}}^\infty + p\int_{0^{-}}^{\infty} e^{-pt} f(t)\,dt\,,$

soit finalement (et de proche en proche ou par récurrence pour les dérivations successives) :

$\mathcal{L}\{f'\} = p \mathcal{L}\{f\} - f(0^{-})$

$\mathcal{L}\{f''\} = p^2 \mathcal{L}\{f\} - p f(0^{-}) - f'(0^{-})$

$\mathcal{L}\left\{ f^{(n)} \right\} = p^n \mathcal{L}\{f\} - p^{n - 1} f(0^{-}) - \cdots - f^{(n - 1)}(0^{-})$

Cette dernière expression peut s'écrire, en désignant l'opérateur $f\left( 0^{-}\right) \mapsto f^{\left( i\right) }\left( 0^{-}\right)$ par $\partial _{0}^{i}$ pour tout entier $i\geq 0$ ,

$\mathcal{L}\left( f^{\left( n\right) }\right) =p^{n}\mathcal{L}\left( f\right) -\frac{p^{n}-\partial _{0}^{n}}{p-\partial _{0}}f\left( 0^{-}\right)$

Notons que, vu la définition donnée plus haut d'une fonction généralisée à support positif (en utilisant la notion de germe), les quantités $f(0^{-}), ..., f^{(n - 1)}(0^{-})$ ne sont pas nulles en général.

Application à la dérivée de la fonction de Heaviside[modifier]

Article détaillé : fonction de Heaviside.

La fonction de Heaviside $\Upsilon$ vaut 0 pour t < 0, 1 pour t > 0 (sa valeur en 0 n'a aucune importance). Cette fonction étant discontinue, elle n'est pas dérivable au sens habituel. En revanche, sa dérivée au sens des distributions est la « fonction » de Dirac $\delta$ . Il vient

$\mathcal{L}\left( \delta \right) =p\mathcal{L}\left( \Upsilon \right) -\Upsilon \left( 0^{-}\right) =1-0=1$ ,

puisque, comme le lecteur le vérifiera aisément,

$\mathcal{L}\left( \Upsilon \right) =\dfrac{1}{p}, \Re \left( p\right) >0$ .

On notera que si l'on remplaçait, dans la formule de la règle de dérivation, $f(0^{-})$ par $f(0^{+})$ , on trouverait $\mathcal{L}\left( \delta \right) = 0$ , ce qui est faux. Ce point est pourtant encore discuté par certains auteurs, bien à tort comme on le voit ici.

Multiplication par une puissance de t[modifier]

$\mathcal{L}\left( t^{n}f\left( t\right) \right) =\left( -1\right) ^{n} \dfrac{d^{n}\mathcal{L}\left\{ f\right\} }{dp^{n}}$

La formule inverse (pour $n = 1$ ) est

$\mathcal{L}\left\{\frac{f(t)}{t} \right\} = \int_p^\infty F(\sigma)\, d\sigma$

et elle est valide à condition que $f$ soit de la forme $t\mapsto tg\left( t\right)$ où $g$ est une fonction généralisée à support positif. Une manière de démontrer ce résultat est indiquée ci-dessous.

[afficher]

démonstration détaillée

Intégration[modifier]

Article détaillé : Intégrale (mathématiques).

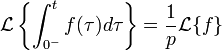
$\mathcal{L}\left\{ \int_{0^{-}}^{t}f(\tau )d\tau \right\} = {1 \over p} \mathcal{L}\{f\}$

et si $f$ est une fonction à support positif, continue sur $\left[ 0,+\infty \right[$ , on a pour tout $a > 0$

$\mathcal{L}\left\{ \int_a^t f(\tau) d\tau \right\} = {1 \over p} \mathcal{L}\{f\}+ {1 \over p}\int_a^0 f(\tau)d\tau$

Valeur finale[modifier]

Si la limite dans le domaine temporel existe, alors :

$\lim_{t \to +\infty} f(t)=\lim_{p \to 0} pF(p)$

Valeur initiale[modifier]

Si la limite dans le domaine temporel existe, alors :

$\lim_{t \to 0+} f(t)=\lim_{p \to +\infty} pF(p)$

Convolution[modifier]

Article détaillé : Produit de convolution.

$\mathcal{L}\{f * g\} = \mathcal{L}\{ f \} \mathcal{L}\{ g \}$

Transformée de Laplace d'une fonction de période T[modifier]

Si $f$ est une fonction nulle pour $t < 0$ et, pour $t > 0$ , périodique de période $T$ ,

$\mathcal{L}\{ f \} = {1 \over 1 - e^{-Tp}} \int_0^T e^{-pt} f(t)\,dt$

§ On peut montrer la formule de la manière suivante :

[afficher]

démonstration détaillée

Tableau résumé des propriétés de la transformée de Laplace[modifier]

[afficher]

Quelques transformées usuelles[modifier]

La transformée de Laplace monolatérale n'est valide que pour des fonctions (éventuellement généralisées) à support positif. C'est pour cette raison que les fonctions temporelles de cette table sont multiples de (ou composées avec) $\Upsilon$ , fonction échelon unité (Heaviside).

[afficher]

table des transformées de Laplace usuelles

Exemple d'utilisation de la transformée de Laplace en électricité[modifier]

On considère un circuit dit « R,C », constituée d'une résistance électrique de valeur R et d'un condensateur de capacité électrique C, placés en série. Dans tout les cas on considère que le circuit n'est placé aux bornes d'un générateur idéal de tension délivrant une tension (en général) variable $u\left(t\right)$ qu'à un instant choisi pour origine des dates, et que le condensateur est initialement déchargé. On a ainsi respectivement pour la charge $q\left(t\right)$ du condensateur et l'intensité dans le circuit $i\left(t\right) \equiv \frac{dq}{dt}$ les conditions initiales suivantes: $q\left( 0^{-}\right) =0 , i\left( 0^{-}\right) =0$ .

Charge d'un condensateur par un échelon de tension[modifier]

On applique la tension $u\left(t\right)$ suivante:

$u\left(t\right) = \begin{cases} 0, \text{ si } t < 0 \\ U_{0} = cte, \text{ si } t \ge 0 \end{cases},$

et l'équation différentielle reliant la réponse $q\left(t\right)$ à l'entrée $u\left(t\right)$ est en appliquant les lois usuelles de l'électricité :

$U_{0}\Upsilon(t) = R\frac{dq}{dt} + \frac{q\left(t\right)}{C},$

soit encore en posant $\tau \equiv RC$ (cette quantité à la dimension d'une durée) :

$\frac{CU_{0}}{\tau} = \frac{q\left(t\right)}{\tau} + \frac{dq}{dt}.$

On prend la transformée de Laplace membre à membre de cette dernière équation, en notant $Q\left(p\right)$ la transformée de $q\left(t\right)$ , il vient (en prenant en compte le fait que $q\left( 0^{-}\right) =0$ ) :

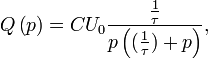
$Q\left(p\right) = CU_{0}\frac{\frac1\tau}{p\left((\frac1\tau) + p\right)},$

ce qui peut aussi s'écrire sous la forme :

$Q\left(p\right) = H\left(p\right)U\left(p\right), \text{ avec } H\left(p\right)\equiv \frac{\left(1/\tau\right)}{\left[\left(1/\tau\right)+p\right]},$ fonction de transfert du système R,C, et $U\left(p\right)=CU_{0}/p,$ transformée de Laplace de l'entrée⁴,

que l'on peut aussitôt inverser en (on utilise l'entrée numéro 3 de la table ci-dessus avec $\alpha = 1/\tau$ ) : $q\left(t\right) = U_{0}C\left[1 - e^{-t /\tau}\right].$ ^5, ⁶

On voit la facilité d'usage de la transformation de Laplace, qui permet de s'abstraire complétement de la résolution de l'équation différentielle dans l'espace des temps par un passage dans « l'espace p ». Par ailleurs, la prise en compte des conditions initiales est effectuée lors de la transformation.

Notes et références[modifier]

Notes[modifier]

1. ↑ Bourlès 2010 (§13.3.4), Bourlès et Marinescu 2011(§7.3.4.1)

2. ↑ Denis-Papin et Kaufmann 1967

3. ↑ Bracewell 2000, Table 14.1, p. 385

4. ↑ en unité de charge de par la multiplication par C

5. ↑ L'interprétation physique de cette solution est très simple : il y a superposition d'un régime transitoire $\scriptstyle{q_{trans} \left(t\right) = - U_{0}Ce^{-t/\tau}}$ , qui décrit la charge progressive du condensateur, la quantité $\scriptstyle{\tau \equiv RC}$ donnant l'échelle de temps (c'est un exemple de temps de relaxation d'un système), à un régime permament $\scriptstyle{Q_perm = CU_{0} \equiv Q_{m}}$ qui correspond à l'état du condensateur complètement chargé sous la tension continue $U_{0}$ . On montre aisément que le condensateur est à 90 % chargé ( $\scriptstyle{q = 0,90 Q_{m}}$ ) au bout de la durée $\scriptstyle{T = \tau\ln{10} \approx 2,3025\tau}$ .

6. ↑ Le terme $\scriptstyle{\left(1-e^{-t/\tau}\right)}$ est la fonction de transfert du système dans le domaine temporel.

Références[modifier]

§ Henri Bourlès, Linear Systems, John Wiley & Sons, 2010, 544 p. (ISBN 1848211627)

§ Henri Bourlès et Bogdan Marinescu, Linear Time-Varying Systems: Algebraic-Analytic Approach, Springer, 2011, 638 p. (ISBN 3642197264)

§ (en) Ronald N. Bracewell, The Fourier Transform and Its Applications, Boston, McGraw-Hill, 2000, 3^e éd. (ISBN 0-07-116043-4).

§ M. Denis-Papin et A. Kaufmann, Cours de calcul opérationnel appliqué, Albin Michel, 1967

§ Laurent Schwartz, Méthodes mathématiques pour les sciences physiques, Hermann, 1965 (ISBN 2705652132)

§ (en) D.V. Widder, The Laplace Transform, Dover Publications, 2011 (ISBN 048647755X)