Induction motor

From Wikipedia, the free encyclopedia

Three-phase totally enclosed fan-cooled (TEFC) induction motor, with and, at right, without end cover to show cooling fan. In TEFC motor, interior losses are dissipated indirectly through enclosure fins mostly by forced air convection.

An induction or asynchronous motor is an AC motor in which all electromagnetic energy is transferred by inductive coupling from a primary winding to a secondary winding, the two windings being separated by an air gap. In three-phaseinduction motors, that are inherently self-starting, energy transfer is usually from the stator to either a wound rotor or ashort-circuited squirrel cage rotor. Three-phase cage rotor induction motors are widely used in industrial drives because they are rugged, reliable and economical. Single-phase induction motors are also used extensively for smaller loads. Although most AC motors have long been used in fixed-speed load drive service, they are increasingly being used invariable-frequency drive (VFD) service, variable-torque centrifugal fan, pump and compressor loads being by far the most important energy saving applications for VFD service. Squirrel cage induction motors are most commonly used in both fixed-speed and VFD applications.

Cutaway view through stator of TEFC induction motor. Note rotor air circulation vanes.

[hide]

· 1 History

· 2 Principle of operation

o 2.1 Synchronous speed

o 2.2 Slip

o 2.3 Torque

§ 2.3.1 Standard torque

§ 2.3.2 Starting

§ 2.3.3 Speed control

· 3 Construction

· 4 Rotation reversal

· 5 Power factor

· 6 Efficiency

· 7 Steinmetz equivalent circuit

· 8 Linear induction motor

· 9 See also

· 10 Notes

· 11 References

· 12 Classical sources

· 13 External links

[edit]History

Squirrel cage rotor

In 1824, the French physicist François Arago formulated the existence of rotating magnetic fields, termed Arago's rotations, which, by manually turning switches on and off, Walter Baily demonstrated in 1879 as in effect the first primitive induction motor.^[1][2][3][4] Practical alternating current induction motors seem to have been independently invented by Galileo Ferraris and Nikola Tesla, a working motor model having been demonstrated by the former in 1885 and by the latter in 1887. Tesla applied for U.S. patents in October and November of 1887 and was granted some of these patents in May 1888. He presented his technical paper A New System for Alternating Current Motors and Transformers to the American Institute of Electrical Engineers (AIEE) soon after that year.^{[5][6][7][8][9]} Tesla's paper described three four-stator-pole motor types: one with a four-pole rotor forming a non-self-starting reluctance motor, another with a wound rotor forming a self-starting induction motor, and the third a true synchronous motor with separately-excited DC supply to rotor winding. Tesla's U.S. Patent 382,279, filed in November 1887, however, described a shorted-winding-rotor induction motor. George Westinghouse promptly bought Tesla’s patents, employed Tesla to develop them, and assigned C. F. Scott to help Tesla.^[5][10][11] In 1888, the Royal Academy of Science of Turin published Ferraris's research detailing the foundations of motor operation while however concluding that "the apparatus based on that principle could not be of any commercial importance as motor."^[12][13][4] Steadfast in his promotion of three-phase development, Mikhail Dolivo-Dobrovolsky's invented the cage-rotor induction motor in 1889 and the three-limb transformer in 1890.^[14][15] However, he claimed that Tesla's motor was not practical because of two-phase pulsations, which prompted him to persist in his three-phase work.^[16] Although Westinghouse achieved its first practical induction motor in 1892 and developed a line of polyphase 60 hertz induction motors in 1893, these early Westinghouse motors were two-phase motors with wound rotors until B. G. Lamme developed a rotating bar winding rotor.^[5] The General Electric Company (GE) began developing three-phase induction motors in 1891.^[5] By 1896, General Electric and Westinghouse signed a cross-licensing agreement for the bar-winding-rotor design, later called the squirrel-cage rotor.^[5] GE's Charles Proteus Steinmetz was the first to make use of the letter "j" (the square root of negative one) to designate the 90 degree rotation operator in electrical mathematical expressions, and to thus be able to describe the induction motor in terms now commonly known as the Steinmetz equivalent circuit.^{[5][17][18][19]} Induction motor improvements flowing from these inventions and innovations were such that a 100 horsepower induction motor currently has the same mounting dimensions as a 7.5 horsepower motor in 1897.^[5]

[edit]Principle of operation

A three-phase power supply provides a rotating magnetic field in an induction motor.

In both induction and synchronous motors, the AC power supplied to the motor's stator creates a magnetic field that rotates in time with the AC oscillations. Whereas a synchronous motor's rotor turns at the same rate as the stator field, an induction motor's rotor rotates at a slower speed than the stator field. The induction motor stator's magnetic field is therefore changing or rotating relative to the rotor. This induces an opposing current in the induction motor's rotor, in effect the motor's secondary winding, when the latter is short-circuited or closed through an external impedance.^[20] The rotating magnetic flux induces currents in the windings of the rotor;^[21] in a manner similar to currents induced in transformer's secondary windings. These currents in turn create magnetic fields in the rotor that react against the stator field. Due to Lenz's Law, the direction of the magnetic field created will be such as to oppose the change in current through the windings. The cause of induced current in the rotor is the rotating stator magnetic field, so to oppose this the rotor will start to rotate in the direction of the rotating stator magnetic field. The rotor accelerates until the magnitude of induced rotor current and torque balances the applied load. Since rotation at synchronous speed would result in no induced rotor current, an induction motor always operates slower than synchronous speed. The difference between actual and synchronous speed or slip varies from about 0.5 to 5% for standard Design B torque curve induction motors.^[22] The induction machine's essential character is that it is created solely by induction instead of being separately excited as in synchronous or DC machines or being self-magnetized as in permanent magnet motors.^[20]

For these currents to be induced, the speed of the physical rotor must be lower than that of the stator's rotating magnetic field ( $n_s$ ), or the magnetic field would not be moving relative to the rotor conductors and no currents would be induced. As the speed of the rotor drops below synchronous speed, the rotation rate of the magnetic field in the rotor increases, inducing more current in the windings and creating more torque. The ratio between the rotation rate of the magnetic field as seen by the rotor (slip speed) and the rotation rate of the stator's rotating field is called slip. Under load, the speed drops and the slip increases enough to create sufficient torque to turn the load. For this reason, induction motors are sometimes referred to as asynchronous motors.^[23] An induction motor can be used as an induction generator, or it can be unrolled to form the linear induction motorwhich can directly generate linear motion.

[edit]Synchronous speed

An AC motor's synchronous speed, $n_s$ , is the rotation rate of the stator's magnetic field, which is expressed in revolutions per minute as

$n_s={120\times{f}\over{p}}$ (RPM),

where $f$ is the motor supply's frequency in Hertz and $p$ is the number of magnetic poles.^[24][25] That is, for a six-pole three-phase motor with three pole-pairs set 120° apart, $p$ equals 6 and $n_s$ equals 1,000 RPM and 1,200 RPM respectively for 50 Hz and 60 Hz supply systems.

[edit]Slip

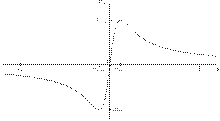
Typical torque curve as a function of slip, represented as 'g' here.

Slip, $s$ , is defined as the difference between synchronous speed and operating speed, at the same frequency, expressed in rpm or in percent or ratio of synchronous speed. Thus

$s = \frac{n_s-n_r}{n_s}\,$

where $n_s$ is stator electrical speed, $n_r$ is rotor mechanical speed.^[8][26] Slip, which varies from zero at synchronous speed and 1 when the rotor is at rest, determines the motor's torque. Since the short-circuited rotor windings have small resistance, a small slip induces a large current in the rotor and produces large torque.^[27] At full rated load, slip varies from more than 5% for small or special purpose motors to less that 1% for large motors.^[28] These speed variations can cause load-sharing problems when differently sized motors are mechanically connected.^[28] Various methods are available to reduce slip, VFDs often offering the best solution.^[28]

[edit]Torque

[edit]Standard torque

Speed-torque curves for four induction motor types: A) Single-phase, B) Polyphase cage, C) Polyphase cage deep bar, D) Polyphase double cage

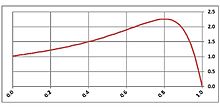
Typical speed-torque curve for NEMA Design B Motor

The typical speed-torque relationship of a standard NEMA Design B polyphase induction motor is as shown in the curve at right. Suitable for most low performance loads such as centrifugal pumps and fans, Design B motors are constrained by the following typical torque ranges:^[22][a]

· Breakdown torque, 175-300 percent of rated torque

· Locked-rotor torque, 75-275 percent of rated torque

· Pull-up torque, 65-190 percent of rated torque.

Over a motor's normal load range, the torque's slope is approximately linear or proportional to slip because the value of rotor resistance divided by slip, $R_r^'/s$ , dominates torque in linear manner.^[29] As load increases above rated load, stator and rotor leakage reactance factors gradually become more significant in relation to $R_r^'/s$ such that torque gradually curves towards breakdown torque. As torque increases beyond breadown torque motor stalls. Although polyphase motors are inherently self-starting, their starting and pull-up torque design limits must be high enough to overcome actual load conditions. In two-pole single-phase motors, the torque goes to zero at 100% slip (zero speed), so these require alterations to the stator such as shaded-poles to provide starting torque.

[edit]Starting

Main article: Motor controller

There are five basic types of competing small induction motor: single-phase capacitor-start, capacitor-run, split-phase and shaded-pole types, and small polyphase induction motors.

A single-phase induction motor requires separate starting circuitry to provide a rotated field to the motor. The normal running windings within such a single-phase motor can cause the rotor to turn in either direction, so the starting circuit determines the operating direction.

In certain smaller single-phase motors, starting is done by mean of a shaded pole with a copper wire turn around part of the pole. The current induced in this turn lags behind the supply current, creating a delayed magnetic field around the shaded part of the pole face. This imparts sufficient rotational field energy to start the motor. These motors are typically used in applications such as desk fans and record players, as the required starting torque is low, and the low efficiency is tolerable relative to the reduced cost of the motor and starting method compared to other AC motor designs.

Larger single phase motors have a second stator winding fed with out-of-phase current; such currents may be created by feeding the winding through a capacitor or having it have different values of inductance and resistance from the main winding. In some designs, the second winding is disconnected once the motor is up to speed, usually either by a centrifugal switch acting on weights on the motor shaft or a thermistor which heats up and increases its resistance, reducing the current through the second winding to an insignificant level. Other designs keep the second winding on when running, improving torque.

Self-starting polyphase induction motors produce torque even at standstill. Available cage induction motor starting methods include direct-on-line starting, reduced-voltage reactor or auto-transformer starting, star-delta starting or, increasingly, new solid-state soft assemblies and, of course, VFDs.^[30]

Polyphase motors have rotor bars shaped to give different speed-torque characteristics. The current distribution within the rotor bars varies depending on the frequency of the induced current. At standstill, the rotor current is the same frequency as the stator current, and tends to travel at the outermost parts of the cage rotor bars (by skin effect). The different bar shapes can give usefully different speed-torque characteristics as well as some control over the inrush current at startup.

In wound rotor motors, rotor circuit connection through slip rings to external resistances allows change of speed-torque characteristics for acceleration control and speed control purposes.

[edit]Speed control

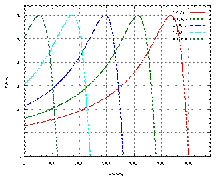
Typical speed-torque curves for different motor input frequencies as for example used with variable-frequency drives.

Before the development of semiconductor power electronics, it was difficult to vary the frequency, and cage induction motors were mainly used in fixed speed applications. Applications such as electric overhead cranes used DC drives or wound rotor motors (WRIM) with slip rings for rotor circuit connection to variable external resistance allowing considerable range of speed control. However, resistor losses associated with low speed operation of WRIMs is a major cost disadvantage, especially for constant loads.^[31] Large slip ring motor drives, termed slip energy recovery systems, some still in use, recover energy from the rotor circuit, rectify it, and return it to the power system using a VFD. In many industrial variable-speed applications, DC and WRIM drives are being displaced by VFD-fed cage induction motors. The most common efficient way to control asynchronous motor speed of many loads is with VFDs. Barriers to adoption of VFDs due to cost and reliability considerations have been reduced considerably over the past three decades such that it is estimated that drive technology is adopted in as many as 30-40% of all newly installed motors.^[32]

[edit]Construction

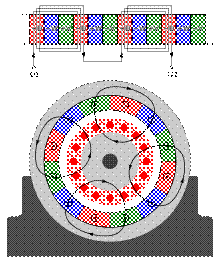
Typical winding pattern for a three-phase (U, V, W), four-pole motor. Note the interleaving of the pole windings and the resulting quadrupole field.

The stator of an induction motor consists of poles carrying supply current to induce a magnetic field that penetrates the rotor. To optimize the distribution of the magnetic field, the windings are distributed in slots around the stator, with the magnetic field having the same number of north and south poles. Induction motors are most commonly run on single-phase or three-phase power, but two-phase motors exist; in theory, induction motors can have any number of phases. Many single-phase motors having two windings can be viewed as two-phase motors, since a capacitor is used to generate a second power phase 90° from the single-phase supply and feeds it to the second motor winding. Single-phase motors require some mechanism to produce a rotating field on startup. Cage induction motor rotor's conductor bars are typically skewed to reduce noise.

[edit]Rotation reversal

The method of changing the direction of rotation of an induction motor depends on whether it is a three-phase or single-phase machine. In the case of three phase, reversal is carried out by swapping connection of any two phase conductors. In the case of a single-phase motor it is usually achieved by changing the connection of a starting capacitor from one section of a motor winding to the other. In this latter case both motor windings are usually similar (e.g. in washing machines).

[edit]Power factor

The power factor of induction motors varies with load, typically from around 0.85 or 0.90 at full load to as low as 0.35 at no-load,^[30] due to stator and rotor leakage and magnetizing reactances.^[33] Power factor can be improved by connecting capacitors either on an individual motor basis or, by preference, on a common bus covering several motors. For economic and other considerations power systems are rarely power factor corrected to unity power factor.^[34] Power capacitors application with harmonic currents requires power system analysis to avoid harmonic resonance between capacitors and transformer and circuit reactances.^[35] Common bus power factor correction is recommended to minimize resonant risk and to simplify power system analysis.^[35]

[edit]Efficiency

(See also Energy savings)

Full load motor efficiency varies from about 85 to 97%, related motor losses being broken down roughly as follows:^[36]

· Friction and windage, 5% – 15%

· Iron or core losses, 15% – 25%

· Stator losses, 25% – 40%

· Rotor losses, 15% – 25%

· Stray load losses, 10% – 20%.

Various regulatory authorities in many countries have introduced and implemented legislation to encourage the manufacture and use of higher efficiency electric motors. There is existing and forthcoming legislation regarding the future mandatory use of premium-efficiency induction-type motors in defined equipment. For more information, see: Premium efficiency and Copper in energy efficient motors.

[edit]Steinmetz equivalent circuit

This section may be too technical for most readers to understand. Please help improve this section to make it understandable to non-experts, without removing the technical details. The talk page may contain suggestions. (December 2012)

Many useful motor relationships between time, current, voltage, speed, power factor and torque can be obtained from analysis of the Steinmetz equivalent circuit (also termed T-equivalent circuit or IEEE recommended equivalent circuit), a mathematical model used to describe how an induction motor's electrical input is transformed into useful mechanical energy output. The equivalent circuit is a single-phase representation of a multiphase induction motor that is valid in steady-state balanced-load conditions.

The Steinmetz equivalent circuit is expressed simply in terms of the following components:

· Stator resistance and leakage reactance ( $R_s$ , $X_s$ ).

· Rotor resistance, leakage reactance, and slip ( $R_r$ , $X_r$ or $R_r^'$ , $X_r^'$ , and $s$ ).

· Magnetizing reactance ( $X_m$ ).

Paraphrasing from Alger in Knowlton, an induction motor is simply an electrical transformer the magnetic circuit of which is separated by an air gap between the stator winding and the moving rotor winding.^[20] The equivalent circuit can accordingly be shown either with equivalent circuit components of respective windings separated by an ideal transformer or with rotor components referred to the stator side as shown in the following circuit and associated equation and parameter definition tables.^{[30][34][37][38][39][40]}

Steinmetz equivalent circuit

[show]Table of Circuit Parameter Definitions

The following rule-of-thumb approximations apply to the circuit:^[40][41][42]

· Maximum current happens under locked rotor current (LRC) conditions and is somewhat less than ${V_s}/X$ , with LRC typically ranging between 6 and 7 times rated current for standard Design B motors.^[22]

· Breakdown torque $T_{max}$ happens when $s\approx{R_r^'/X}$ and $I_s\approx{0.7}LRC$ such that $T_{max}\approx{K*V_s^2}/(2X)$ and thus, with constant voltage input, a low-slip induction motor's percent-rated maximum torque is about half its percent-rated LRC.

· The relative stator to rotor leakage reactance of standard Design B cage induction motors is^[43]

$\frac{X_s}{X_r^'}\approx\frac{0.4}{0.6}$ .

· Neglecting stator resistance, an induction motor's torque curve reduces to the Kloss equation^[44]

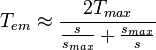$T_{em}\approx\frac{2T_{max}}{\frac{s}{s_{max}}+\frac{s_{max}}{s}}$ , where $s_{max}$ is slip at $T_{max}$ .

[show]Table of Basic Electrical Equations

[show]Table of Power Equations

[show]Table of Torque Equations

[edit]Linear induction motor

Main article: linear induction motor

Linear induction motors, that work on same general principles as rotary induction motors and are frequently three-phase, are designed to produce straight line motion. Uses includemagnetic levitation, linear propulsion, linear actuators, and liquid metal pumping.^[45]

[edit]See also

Machine asynchrone

Machine asynchrone de 8 kW.

La machine asynchrone, connue également sous le terme « anglo-saxon » de machine à induction, est une machine électrique à courant alternatif sans connexion entre le stator et le rotor. Les machines possédant un rotor « en cage d'écureuil » sont aussi connues sous le nom de machines à cage ou machines à cage d'écureuil. Le terme asynchroneprovient du fait que la vitesse de rotation du rotor de ces machines n'est pas exactement déterminée par la fréquence descourants qui traversent leur stator (voir : « Principes généraux – Glissement d'une machine asynchrone »).

La machine asynchrone a longtemps été fortement concurrencée par la machine synchrone dans les domaines de forte puissance, jusqu'à l'avènement de l'électronique de puissance. La machine asynchrone est utilisée aujourd'hui dans de nombreuses applications, notamment dans le transport (métro, trains, propulsion des navires, automobiles électriques), dans l'industrie (machines-outils), dans l'électroménager. Elle était à l'origine uniquement utilisée en moteur mais, toujours grâce à l'électronique de puissance, elle est de plus en plus souvent utilisée en génératrice¹, par exemple dans les éoliennes².

Pour fonctionner en courant monophasé, les machines asynchrones nécessitent un système de démarrage. Pour les applications de puissance, au-delà de quelques kilowatts, les moteurs asynchrones sont uniquement alimentés par des systèmes de courants triphasés.

Sommaire

[masquer]

· 1 Historique

· 2 Présentation

· 3 Principes généraux

o 3.1 Glissement d'une machine asynchrone

o 3.2 Plaque signalétique d'un moteur asynchrone

o 3.3 Variateur de vitesse

o 3.4 Démarrage

§ 3.4.1 Démarrage sous tension réduite

§ 3.4.1.1 Démarrage étoile-triangle

§ 3.4.1.2 Démarrage par auto-transformateur

§ 3.4.1.3 Démarrage résistif

§ 3.4.2 Démarrage à tension nominale

§ 3.4.2.1 Démarrage rotorique

§ 3.4.2.2 Moteur Boucherot type α

o 3.5 Freinage

o 3.6 Applications

· 4 Machine asynchrone triphasée

o 4.1 Constitution

§ 4.1.1 Réalisation du stator

§ 4.1.2 Réalisation du rotor

o 4.2 Modélisation et mise en équation

§ 4.2.1 Méthode utilisée

§ 4.2.4.1 Flux à travers un enroulement statorique

§ 4.2.4.2 Flux à travers un enroulement rotorique

§ 4.2.5 Les tensions

§ 4.2.5.1 Tension aux bornes d'une phase du stator

§ 4.2.5.2 Tension aux bornes d'une phase du rotor

o 4.3 Schémas équivalents

§ 4.3.1 Schéma général

§ 4.3.2 Schéma ramené au stator

§ 4.3.3 Prise en compte des pertes fer

§ 4.3.4 Identifications des éléments du schéma équivalent

§ 4.3.4.1 Essai en continu

§ 4.3.4.2 Essai au synchronisme : g = 0

§ 4.3.4.3 Essai rotor bloqué et tension réduite : g = 1

o 4.4 Caractéristiques électromécaniques

§ 4.4.1 Machine alimentée par un système de tensions de fréquence fixe

§ 4.4.1.1 Couple électromagnétique en fonction du glissement

§ 4.4.1.2 Couple électromagnétique en fonction de la vitesse de rotation

§ 4.4.1.3 Les domaines de fonctionnement de la machine asynchrone

§ 4.4.2 Machine alimentée par un onduleur

§ 4.4.2.1 Commande en U/f

§ 4.4.2.1.1 Principe

§ 4.4.2.1.2 Mise en équation

§ 4.4.2.1.3 Remarques

§ 4.4.2.1.4 Inconvénients

§ 4.4.2.2 Commande vectorielle

o 4.5 Bilans de puissance

§ 4.5.1 Bilan de puissance de la machine fonctionnant en moteur

§ 4.5.2 Bilan de puissance de la machine fonctionnant en génératrice

· 5 Machine asynchrone monophasée

o 5.1 Dispositifs de démarrage

· 6 Raccordement

· 7 Notes et références

· 8 Annexes

o 8.1 Bibliographie en langue française

o 8.2 Articles connexes

o 8.3 Liens externes

Historique[modifier]

La paternité de la machine asynchrone est controversée. Elle pourrait être attribuée à trois inventeurs :

· en 1887, Nikola Tesla dépose un brevet sur la machine asynchrone^3,4, puis en mai de l'année suivante cinq autres brevets.

· Pendant la même période Galileo Ferraris publie des traités sur les machines tournantes, avec une expérimentation en 1885, puis une théorie sur le moteur asynchrone enavril 1888⁵.

· En 1889, Mikhaïl Dolivo-Dobrovolski, électricien allemand d'origine russe, invente le premier moteur asynchrone à courant triphasé à cage d'écureuil qui sera construit industriellement à partir de 1891⁶.

Du fait de sa simplicité de construction, d'utilisation et d'entretien, de sa robustesse et son faible prix de revient, la machine asynchrone est aujourd'hui très couramment utilisée comme moteur dans une gamme de puissance allant de quelques centaines de watts à plusieurs milliers de kilowatts.

Quand la machine asynchrone est alimentée par un réseau à fréquence fixe, il est difficile de faire varier sa vitesse. En outre, au démarrage, le couple est faible et le courant appelé est très élevé. Deux solutions historiques ont résolu ce dernier problème : le rotor à encoches profondes et le rotor à double cage mis au point en 1912 par Paul Boucherot.

Grâce aux progrès de l'électronique de puissance, l'alimentation par un onduleur à fréquence variable permet maintenant de démarrer la machine convenablement et de la faire fonctionner avec une vitesse réglable dans une large plage. C'est pourquoi il est utilisé pour la motorisation des derniers TGV ainsi que des nouveaux métros parisiens^7,8.

Intérieur d'une machine asynchrone diphasée,R. Alioth et Cie, n^o 1042, vers 1893.

Le stator, 4 paires de pôles.
Les deux borniers de raccordement.

Le rotor, cage constituée de bobinages de cuivre en court-circuit. Les encoches sont légèrement inclinées.

Présentation[modifier]

Rotor (à gauche) et stator (à droite) d'une machine asynchrone 0,75 kW.

La machine se compose de deux pièces principales :

· Le stator est une pièce construite en matériau ferromagnétique, servant de support et incluant un bobinage relié au réseau ou à unvariateur de vitesse.

· Le rotor est un cylindre en matériau ferromagnétique fixé au stator par des paliers. Il comporte un enroulement constitué de conducteurs en court-circuit parcourus par des courants induits par le champ magnétique créé par les courants statoriques. C'est la principale différence avec une machine synchrone, laquelle a un rotor avec un champ magnétique provenant d'aimants permanents ou de bobines alimentées en courant continu.

Cette machine peut, selon sa construction, être alimentée par un réseau monophasé ou polyphasé (généralement triphasé car c'est celui de la distribution).

La machine asynchrone est la machine électrique la plus utilisée dans le domaine des puissances supérieures à quelques kilowatts car elle offre alors le meilleur rapport qualité prix. Surtout depuis l'apparition dans les années 1970 de variateurs permettant de faire varier la fréquence de rotation du moteur dans une large gamme⁹.

Bien que réversible, la machine asynchrone est principalement (mais pas exclusivement) utilisée en moteur.

Principes généraux[modifier]

Les courants statoriques créent un champ magnétique tournant dans le stator. La fréquence de rotation de ce champ est imposée par la fréquence des courants statoriques, c’est-à-dire que sa vitesse de rotation est proportionnelle à la fréquence de l'alimentation électrique. La vitesse de ce champ tournant est appelée vitesse de synchronisme.

L'enroulement au rotor est donc soumis à des variations de flux (du champ magnétique). Une force électromotrice induite apparaît qui crée des courants rotoriques. Ces courants sont responsables de l'apparition d'un couple qui tend à mettre le rotor en mouvement afin de s'opposer à la variation de flux : loi de Lenz. Le rotor se met donc à tourner pour tenter de suivre le champ statorique.

La machine est dite asynchrone car elle est dans l'impossibilité, sans la présence d'un entraînement extérieur, d'atteindre la même vitesse que le champ statorique. En effet, dans ce cas, vu dans le référentiel du rotor, il n'y aurait pas de variation de champ magnétique ; les courants s'annuleraient, de même que le couple qu'ils produisent, et la machine ne serait plus entraînée. La différence de vitesse entre le rotor et le champ statorique est appelée vitesse de glissement.

Lorsqu'il est entraîné au-delà de la vitesse de synchronisme — fonctionnement hypersynchrone — la machine fonctionne en générateur alternatif. Mais son stator doit être forcément relié au réseau car lui seul peut créer le champ magnétique nécessaire pour faire apparaître les courants rotoriques.

Un fonctionnement en générateur alternatif autonome est toutefois possible à l'aide de condensateurs connectés sur le stator, à condition qu'il existe un champ magnétique rémanent. On retrouve cette même problématique lorsqu'on cherche à faire fonctionner des machines à courant continu à excitation série en génératrice. À défaut, des dispositifs d'électronique de puissance et une batterie permettent d'amorcer le fonctionnement en génératrice autonome. Cette solution est mise en œuvre pour produire de l'électricité à l'aide d'éoliennes ou de groupes électrogènes, constitués d'une génératrice couplée à un moteur à combustion interne.

Glissement d'une machine asynchrone[modifier]

Le glissement est une grandeur qui rend compte de l'écart de vitesse de rotation d'une machine asynchrone par rapport à la vitesse de rotation de son champ statorique. Il doit y avoir une différence de vitesse pour que ce type de moteur fonctionne car c'est le décalage entre le rotor et le champ statorique qui provoque l'apparition des courants induits au rotor, courants qui créent le champ rotorique. Il est toutefois possible, par exemple pour réaliser des mesures qui permettent d'identifier les caractéristiques de la machines (essai au synchronisme), d'atteindre la vitesse de synchronisme en utilisant un dispositif comportant au moins un deuxième moteur (par exemple un moteur synchrone), qui assurera la production du couple nécessaire au maintien de la rotation.

En régime, le glissement est toujours faible, de l'ordre de quelques pour cents : de 2 % pour les machines les plus grosses à 6 ou 7 % pour les petites machines triphasées, il peut atteindre 10 % pour les petites machines monophasées. Les pertes par effet Joule dans le rotor étant proportionnelles au glissement, une machine de qualité se doit de fonctionner avec un faible glissement.

· On désigne par $n_s$ la fréquence de rotation du champ statorique dans la machine.

· On désigne par $n$ la fréquence de rotation de la machine.

La fréquence de synchronisme est toujours un sous-multiple entier de la fréquence de l'alimentation électrique :

· En 50 Hz c'est un sous-multiple de 3 000 tr/min, soit : 3 000 ; 1 500 ; 1 000 ; 750, etc.

· En 60 Hz c'est un sous-multiple de 3 600 tr/min, soit : 3 600 ; 1 800 ; 1 200 ; 900, etc.

Soit $p$ le nombre de paires de pôles de la machine et $f$ la fréquence de l'alimentation. On a :

$n_s = \frac fp$ en tr/s ou $n_s = \frac {60 f}{p}$ en tr/min.

Le glissement correspond à la différence de vitesse entre le rotor et le champ statorique exprimée sous la forme d'un pourcentage de la fréquence de rotation.

$n_s - n = g \cdot n_s$ , soit $g = \frac{n_s-n}{n_s}$

Le glissement peut aussi être calculé à partir des vitesses angulaires

$g = \frac{\omega_s-\omega}{\omega_s}$ avec :

· $\omega_s$ la vitesse angulaire de synchronisme du champ statorique dans la machine.

· $\omega$ la vitesse angulaire de rotation de la machine.

Plaque signalétique d'un moteur asynchrone[modifier]

Exemple de plaque signalétique d'un moteur asynchrone triphasé industriel :

Mot 3~ 50/60 Hz	IEC34	IP55
MT90L24-4
1,5 / 1,75 k W		1 420 / 1 710 tr/min
380-420 / 440-480 V - Y		3,7 / 3,6 A
220-240 / 250-280 V - Δ		6,4 / 6,3 A
		cos φ = 0,75 / 0,78

Moteur triphasé utilisable en 50 Hz et 60 Hz	Plaque établie conformément à la norme internationale IEC34	Classement IP (Indice de protection)
Référence constructeur précisant notamment : · la taille de la carcasse moteur · le nombre de pôles
Puissance utile nominale		Fréquence de rotation nominale
Tension entre phase du réseau d'alimentation pour un couplage étoile		Courant de ligne nominal pour un couplage étoile
Tension entre phase du réseau d'alimentation pour un couplage triangle		Courant de ligne nominal pour un couplage triangle
		Facteur de puissance au régime nominal

· Soit on dispose d'un réseau d'alimentation correspondant aux valeurs de tension de la troisième ligne et on doit réaliser un couplage étoile symbolisé par Y (cas le plus fréquent), soit on dispose d'un réseau d'alimentation correspondant aux valeurs de tension de la quatrième ligne et on doit réaliser un couplage triangle symbolisé par Δ. Sur la même ligne, la plaque signalétique indique pour chacun des couplages la valeur de l'intensité du courant de ligne qui sera absorbée au régime nominal.

· À l'aide de grandeurs électriques fournies : tensions entre phases, intensités des courants de ligne et facteur de puissance, il est possible de calculer la puissance active absorbée et d'en déduire le rendement de la machine fonctionnant au régime nominal.

En monophasé :

$P_a =\ U I \cdot \cos \varphi \,$

En triphasé :

$P_a =\sqrt 3 \cdot U I \cdot \cos \varphi \,$

Le rendement :

$\eta =\frac{P_u}{P_a} \,$

Variateur de vitesse[modifier]

La gamme des variateurs de vitesse d'ABB.

Un variateur de vitesse est un équipement électrotechnique alimentant un moteur électrique de façon à pouvoir faire varier sa vitesse de manière continue, de l'arrêt jusqu’à sa vitesse nominale. La vitesse peut être proportionnelle à une valeur analogique fournie par un potentiomètre, ou par une commande externe : un signal de commande analogique ou numérique, issue d'une unité de contrôle. Un variateur de vitesse est constitué d'un redresseur combiné à un onduleur. Le redresseur va permettre d'obtenir un courant quasi continu. À partir de ce courant continu, l'onduleur (bien souvent à modulation de largeur d'impulsion ou MLI¹⁰) va permettre de créer un systèmetriphasé de tensions alternatives dont on pourra faire varier la valeur efficace et la fréquence¹¹.

Le fait de conserver le rapport de la valeur efficace du fondamental de la tension par la fréquence (U₁/f) constant permet de maintenir unflux tournant constant dans la machine, le couple maximun constant et donc de maintenir constante la fonction reliant la valeur du couple en fonction de (n_s - n) (voir § 3-4-2-1 ci-dessous).

Article détaillé : Variateur de vitesse (électricité).

Démarrage[modifier]

Lors d'un démarrage d'une machine asynchrone, le courant d'enclenchement peut atteindre plusieurs fois le courant nominal de la machine^12,13. Si l'application utilise un variateurou un démarreur, c'est ce dernier qui se chargera d'adapter les tensions appliquées à la machine afin de limiter ce courant. En l'absence de variateur de vitesse, il existe plusieurs méthodes permettant de limiter le courant de démarrage. Elles ont été développées avant l'apparition de l'électronique de puissance mais sont encore utilisées de nos jours dans les installations anciennes ou par mesure d'économie pour des applications ne nécessitant pas de variateur en dehors du démarrage.

Démarrage sous tension réduite[modifier]

Plusieurs dispositifs permettent de réduire la tension aux bornes des enroulements du stator pendant la durée du démarrage du moteur ce qui est un moyen de limiter l'intensité du courant de démarrage. L'inconvénient est que le couple moteur est également diminué et que cela augmente la durée avant laquelle la machine atteint le régime permanent.

Démarrage étoile-triangle[modifier]

Lors d'un démarrage étoile-triangle, la machine est d'abord connectée au réseau avec un couplage étoile, puis une fois démarrée, on passe sur couplage triangle¹⁴. Le fait de démarrer avec un couplage étoile permet de diviser par $\sqrt 3$ la tension appliquée¹⁴. Ainsi, le courant maximal absorbé est trois fois plus faible que lors d'un démarrage directement avec un couplage triangle¹⁴. Le couple de démarrage est lui aussi trois fois plus faible que lors d'un démarrage en triangle. La surintensité lors du passage étoile-triangle est inférieure au courant d'appel d'un démarrage effectué directement en triangle.

Réalisée simplement à l'aide de contacteurs, cette méthode de démarrage est très économique.

Démarrage par auto-transformateur[modifier]

Dans ce mode de démarrage, le stator de la machine asynchrone est relié à un auto-transformateur qui permet d'effectuer un démarrage sous tension variable. La tension est progressivement augmentée, l'intensité du courant ne dépassant pas la valeur maximale désirée.

Démarrage résistif[modifier]

Lors d'un démarrage résistif, on insère des résistances en série avec les enroulements statoriques ce qui a pour effet de limiter la tension à leurs bornes. Une fois le démarrage effectué, on court-circuite ces résistances¹⁴. Cette opération peut être effectuée progressivement par un opérateur à l'aide de rhéostats de démarrage.

Démarrage à tension nominale[modifier]

Démarrage rotorique[modifier]

Lors d'un démarrage rotorique, des résistances de puissance sont insérées en série avec les enroulements du rotor. Ce type de démarrage permet d'obtenir un fort couple de démarrage avec des courants de démarrage réduits mais il ne peut être mis en œuvre qu'avec des machines à rotor bobiné muni de contacts glissants (bagues et balais) permettant les connexions électriques des enroulements rotoriques¹⁴. Ces machines sont d'un prix de revient plus important que leurs homologues dits à « cage d'écureuil ».

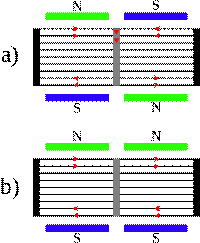
Moteur Boucherot type α[modifier]

Schéma de principe du moteur Boucherot type α

Les moteurs Boucherot type α ont comme particularité d'avoir un stator divisé en deux. Un des stators est fixe, l'autre peut tourner d'un pas polaire. Le rotor, quant à lui, est doté d'une bague très résistive en son centre. Le démarrage se passe ainsi : dans un premier temps, on décale d'un pas polaire les deux stators. Les courants induits créés par chaque stator sont de directions opposées, ils se rebouclent donc au centre du rotor par la bague très résistive. Au fur et à mesure du démarrage, on décale le demi-moteur mobile afin que les courants induits qu'il crée soient dans le même sens que ceux du moteur fixe. À la fin, les courants créés par les deux demi-stators sont dans le même sens et ne passent plus par la bague très résistive¹⁵.

Ce type de dispositif, bien que permettant de faire varier la résistance rotorique sans avoir recours à un rotor bobiné, n'est plus utilisé à cause de sa complexité.

Freinage[modifier]

On distingue plusieurs types de freinage :

· Arrêt en roue libre : (mise hors tension du stator).

· Arrêt piloté : tension statorique progressivement passée à tension nulle.

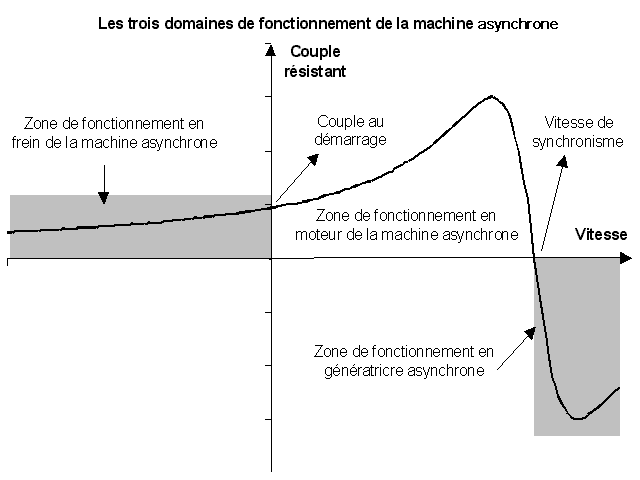
· Freinage hypersynchrone : lorsque la vitesse du rotor est supérieure à la vitesse du champ tournant, le moteur freine. Couplé à un variateur de fréquence qui diminue progressivement la vitesse du moteur on peut arrêter un moteur. Le couple de freinage est élevé à condition de générer un champ correspondant à la valeur de glissement optimal du fonctionnement en génératrice (voir les trois domaines de fonctionnement de la machine asynchrone) et de maintenir la décélération dans ce domaine jusqu'à arrêt complet. Cette méthode est particulièrement efficace pour freiner rapidement une machine asynchrone sans dispositif mécanique additionnel.

· Arrêt par injection de courant continu : L'alimentation en courant continu du stator crée un champ fixe dans la machine qui s'oppose au mouvement

¹⁴. Ce n'est pas la méthode la plus efficace pour freiner la machine (fonctionnement en génératrice décrochée) et les contraintes en courant sont également très sévères. La commande de l'intensité du courant continu permet de piloter le freinage.

· Arrêt à contre-courant :

Le principe consiste à inverser deux phases pendant un court instant¹⁴. Ceci est donc équivalent à un freinage hypersynchrone à fréquence fixe et mal géré. Le couple résistant est faible et le courant appelé est également très important (de l'ordre de 10 à 12 fois l'intensité nominale). La conséquence en est que les enroulements du moteur risquent un sur-échauffement : il est conseillé de prévoir des résistances supplémentaires afin de diminuer l'intensité¹⁴. Enfin, avec cette méthode, le couple décélérateur reste négatif même lorsque la vitesse est égale à 0 tr/min, il faut donc prévoir de couper l'alimentation quand la vitesse est nulle (temporisation, contact centrifuge), sinon la rotation s'inverse¹⁴.

· Freinage mécanique par électro-frein : ce système est constitué d'un frein à disque solidaire de l'arbre de la machine asynchrone et dont les mâchoires initialement serrées hors tension sont commandées par un électroaimant¹⁴. Après alimentation de l'électroaimant, les mâchoires se desserrent laissant la rotation libre. La coupure de l'alimentation provoque le freinage. Ce dispositif aussi appelé « frein à manque de courant » est souvent prévu comme dispositif d'arrêt d'urgence¹⁴.

Applications[modifier]

· Traction électrique (Eurostar, TGV POS, TGV Duplex Dasye notamment)

· Propulsion des navires

· Propulsion électrique automobile (Tesla Roadster notamment)

· Machines-outils

· Ascenseurs

· Treuils

· Pompes

· Électroménager

· Chariots élévateurs

Machine asynchrone triphasée[modifier]

Animation d'une machine asynchrone à cage d'écureuil.

Constitution[modifier]

Réalisation du stator[modifier]

Il est constitué d'un cylindre ferromagnétique entaillé d'encoches permettant d'y loger les bobinages. Ce cylindre est constitué d'un empilement de plaques de tôles feuilletées afin de limiter les courants de Foucault.

Il est courant de réaliser une protection supplémentaire contre les échauffements anormaux des bobinages en plaçant au cœur de ceux-ci soit un disjoncteur thermique, soit un capteur de température, ceci afin de couper l'alimentation électrique en cas de dépassement d'un seuil déterminé de température.

Afin de réaliser le branchement du moteur au réseau, toutes les connexions sont regroupées dans un boîtier, généralement appelé par les électriciens, plaque à bornes. On y retrouve donc six connexions pour les enroulements statoriques, plus éventuellement celles du capteur de température.

Stator d'une machine triphasée

Stator feuilleté sans les bobinages

Diagramme de connexion d'un moteur triphasé

Réalisation du rotor[modifier]

On peut distinguer 4 types de rotor :

· À cage : (rotor en court-circuit) : C'est le plus fréquent. Ce type de rotor a été inventé par Michail Ossipowitsch Doliwo-Dobrowolski au début des années 1890. Ces rotors sont constitués de tôles ferromagnétiques et de barres conductrices régulièrement réparties à la périphérie du rotor. Les barres sont reliées entre elles par deux anneaux de court-circuit (voir figures ci-contre). Les tôles ferromagnétiques servent à guider les lignes de champ tandis que les barres accueillent les courants induits. Pour les moteurs de faible puissance, les rotors sont réalisés à partir d'un empilement de tôles découpées et isolées les unes des autres (feuilletage) dans lesquelles on injecte un matériau conducteur de manière à constituer les barres ainsi que les anneaux de court-circuit. Pour les moteurs de forte puissance, les barres sont insérées dans le rotor puis les anneaux de court-circuit sont soudés ou brasés aux barres¹⁶. Le matériau constituant les barres et les anneaux de court-circuit est généralement un alliage à base d'aluminium, mais on peut aussi rencontrer du cuivre ou du laiton. En général, les barres sont légèrement inclinées suivant l'axe du rotor afin que le nombre de barres présentes sous une phase statorique soit constant quelle que soit la position du rotor. Ce procédé permet de diminuer la variation de la réluctance du circuit magnétique au cours de la rotation du rotor (ou « effet d'encoches ») et de diminuer ainsi les oscillations de couple. C'est cette inclinaison des encoches qui donne à l'ensemble barres plus anneaux de court-circuit la forme d'une cage d'écureuil déformée.

Différentes formes de barres

Couple d'une machine asynchrone pour un rotor à cage et un rotor à encoches profondes

· À double cage : le rotor est construit suivant le principe du rotor à cage simple, mais avec deux cages électriquement indépendantes. Une cage externe à la périphérie du rotor est composée de matériaux résistifs (laiton, bronze) et possède une faible dispersion magnétique. Une cage interne en cuivre possède une résistivité plus faible et une dispersion magnétique importante. La cage externe, surtout active au démarrage, permet d'obtenir un couple plus important dans cette phase de fonctionnement, tandis qu'à régime nominal la cage interne permet de retrouver les caractéristiques d'un rotor à simple cage¹⁷.

· À double encoche ou à encoches profondes : ce sont des rotors à cage qui utilisent l'effet de peau dans les conducteurs afin de faire varier la résistance du rotor en fonction de la vitesse de fonctionnement de la machine. L'effet de peau est un phénomène électromagnétique qui fait que plus la fréquence des courants augmente, plus le courant a tendance à ne circuler qu'en surface des conducteurs. Ainsi, au démarrage, la fréquence des courants rotoriques est égale à celle de l'alimentation et le courant n'utilise que la partie supérieure de la barre. Puis, au fur et à mesure que la vitesse de rotation du rotor augmente, la fréquence des courants rotoriques diminue et le courant utilise une surface de plus en plus importante des barres. Ces topologies de rotor permettent un démarrage avec un couple plus important lorsque la machine est alimentée par une source de tension fixe (sans variateur).

· À bague : le rotor d'une machine à bague est constitué de trois bobines (on parle aussi de rotor bobiné). Chaque bobine est reliée à unebague. Les bagues permettent d'avoir une liaison électrique avec les bobines du rotor. Ce type de rotor a été conçu pour permettre la variation de résistance du rotor en insérant des résistances en série avec les bobines afin de réaliser un démarrage rotorique. Ce dispositif a ensuite permis la variation de vitesse avec un rendement acceptable au moyen d’un procédé appelé cascade hyposynchrone. Le coût élevé et l’apparition des variateurs de fréquence a rendu obsolète ce type de machine.

Structure d'un rotor en cage d'écureuil

Rotor en cage d'écureuil

Coupe d'un rotor à cage à encoches profondes

Tôle utilisée pour la réalisation d'une cage à double encoche]

Modélisation et mise en équation[modifier]

Méthode utilisée[modifier]

Il est très difficile, pour une charge donnée et à partir des tensions et des impédances, de calculer les courants dans la machine et d'en déduire le couple et la fréquence de rotation.

Comme pour ces labyrinthes que l'on trouve dans les journaux, il est plus facile de partir du but à atteindre et de remonter vers le départ. On considère donc que l'on connaît les courants. À partir de l'expression des courants statoriques et rotoriques on déduit les flux du champ magnétique qu'ils produisent. Connaissant les courants et les flux, on écrit l'expression des tensions en appliquant la loi d'Ohm et la loi de Faraday, puis on identifie.

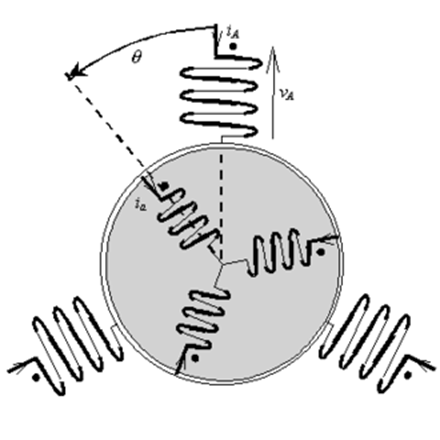
Notations[modifier]

On considère que la machine possède une seule paire de pôles¹⁸.

· Toutes les grandeurs statoriques sont repérées soit par l'indice _S soit par des indices en majuscule.

· Toutes les grandeurs rotoriques sont repérées soit par l'indice _r soit par des indices en minuscule.

l'angle $\theta (t) = \Omega_m .t \,$ correspond au décalage angulaire entre le stator et le rotor. On a :

la vitesse angulaire $\Omega_m = \omega_S - \omega_r = (1-g) . \omega_S \,$

Hypothèses :
Son circuit magnétique est homogène et non saturé. Ses diverses inductances sont constantes. Elle est aussi parfaitement équilibrée :

· les courants des trois phases statoriques ont la même valeur efficace I_S.

· les courants des trois phases rotoriques ont la même valeur efficace I_r.

Les courants[modifier]

Représentation schématique de la machine.

Au stator[modifier]

On fixe l'origine des temps de manière à ce que l'on puisse écrire :

$i_A (t) = I_S \sqrt{2} . \cos \alpha_S \,$

On en déduit les courants des deux autres phases du stator :

$i_B (t) = I_S \sqrt{2} . \cos (\alpha_S - \frac{2 \pi}{3}) \,$

$i_C (t) = I_S \sqrt{2} . \cos (\alpha_S + \frac{2 \pi}{3}) \,$

Avec : $\alpha_S = \omega_S . t \,$ , et $\omega_S \,$ : pulsation des courants statoriques.

Au rotor[modifier]

$i_a (t) = I_r \sqrt{2} . \cos \alpha_r \,$

$i_b (t) = I_r \sqrt{2} . \cos (\alpha_r - \frac{2 \pi}{3}) \,$

$i_c (t) = I_r \sqrt{2} . \cos (\alpha_r + \frac{2 \pi}{3}) \,$

Avec : $\alpha_r= (\omega_r . t - \alpha) \,$ , $\omega_r = g. \omega_S \,$ : pulsation des courants rotoriques, et $\alpha \,$ = phase à l'origine de $i_a \,$ donc variable car l'origine des temps est fixée par $i_A \,$ .

Les flux[modifier]

Notations :

· $L_S ; L_r \,$ : Inductances propres d'un enroulement du stator ; d'un enroulement du rotor.

· $M_S ; M_r \,$ : Inductance mutuelle entre deux enroulements du stator ; entre deux enroulements du rotor.

· $M_{rS} \,$ : Valeur maximale de l'inductance mutuelle entre un enroulement du rotor et un du stator (correspondant à une position pour laquelle θ = 0 ± 2π/3.

Flux à travers un enroulement statorique[modifier]

Le flux à travers la phase A du stator est :

$\Phi_A = (L_S - M_S) i_A + \frac{3}{2} M_{rS}I_r \sqrt{2} \cos (\omega_S . t - \alpha) \,$

[afficher]

Détail des calculs

On pose:

· $(L_S - M_S) = \mathcal{L}_S \,$ : inductance cyclique

· $\frac{3}{2} M_{rS} = \mathcal{M}_{rS} \,$ : inductance mutuelle cyclique

Ces grandeurs cycliques permettent d'isoler chaque phase comme si elle était seule, comme si le flux qui la traverse ne dépendait que du seul courant qui alimente cette phase. L'introduction de ces grandeurs cycliques va permettre d'établir des modèles monophasés équivalents.

On pose également :

· $I'_r \,$ : Courant fictif de valeur efficace $I_r \,$ mais de fréquence $f_S \,$ et d'argument $- \alpha,$

L'expression du flux devient alors plus simple. On applique la transformation complexe et l'on obtient le flux complexe d'une phase du stator :

$\underline \Phi_A = \mathcal{L}_S \underline I_S + \mathcal{M}_{rS} \underline I'_r \,$ à la pulsation $\omega_S \,$

Flux à travers un enroulement rotorique[modifier]

Le calcul du flux rotorique se mène de manière identique avec une différence de signe.

$\Phi_a = (L_r - M_r) i_a + M_{rS} \cos \theta \cdot i_A + M_{rS} \cos (\theta - \frac{2 \pi}{3}) \cdot i_B + M_{rS} \cos (\theta + \frac{2 \pi}{3}) \cdot i_C \,$

Avec l'introduction des grandeurs cycliques

$\Phi_a = \mathcal{L}_r i_a + \frac{3}{2} M_{rS}I_S \sqrt{2} \cos (\theta - \alpha_S) \,$

$= \mathcal{L}_r I_r \sqrt{2} \cos (\omega_r t - \alpha) + \mathcal{M}_{rS} I_S \sqrt{2} \cos (\omega_r t) \,$

Le flux à travers un enroulement rotorique s'écrit :

$\underline \Phi_a = \mathcal{L}_r \underline I_r + \mathcal{M}_{rS} \underline I'_S \,$ à la pulsation $\omega_r \,$

Les tensions[modifier]

Tension aux bornes d'une phase du stator[modifier]

$\underline V_A = R_S . \underline I_A + \frac{d \underline \Phi_A}{dt} \,$

$\underline V_A = (R_S + j \omega_S \mathcal{L}_S) \underline I_S + j \omega_S \mathcal{M}_{rS} \underline I'_r \,$

Tension aux bornes d'une phase du rotor[modifier]

Le rotor est en court-circuit.

$\underline V_a = 0 = R_r . \underline I_a + \frac{d \underline\Phi_a}{dt} \,$

$0 = (R_r + j \omega_r \mathcal{L}_r) \underline I_r + j \omega_r \mathcal{M}_{rS} \underline I'_S \,$

Comme on a $\omega_r = g . \omega_S \,$ , on obtient :

$0 = (\frac{R_r}{g} + j \omega_S \mathcal{L}_r) \underline I_r + j \omega_S \mathcal{M}_{rS} \underline I'_S \,$

Schémas équivalents[modifier]

Sous le vocable schéma équivalent, on désigne un circuit électrique composé de dipôles linéaires permettant de modéliser la machine réelle. Le schéma équivalent le plus pertinent est fonction du domaine d'utilisation et du degré de précision nécessaire. Dans le cas des machines asynchrones, il comprend, au minimum, une association de résistances et d'inductances.

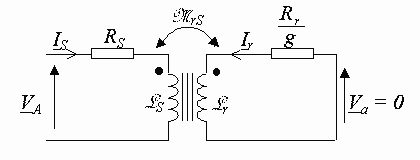
Schéma général[modifier]

Les deux équations suivantes :

· $\underline V_A = (R_S + j \omega_S \mathcal{L}_S) \underline I_S + j \omega_S \mathcal{M}_{rS} \underline I'_r \,$

· $0 = (\frac{R_r}{g} + j \omega_S \mathcal{L}_r) \underline I_r + j \omega_S \mathcal{M}_{rS} \underline I'_S \,$

correspondent à un schéma équivalent ne comportant que des tensions et des courants ayant une fréquence identique à celle de l'alimentation qui alimente la machine et dont le schéma est le suivant :

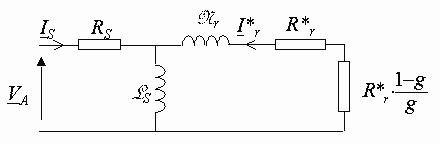
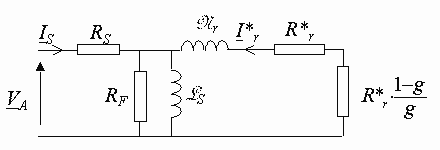
Schéma ramené au stator[modifier]

Les circuits magnétiquement couplés peuvent être transformés en de nombreux schémas équivalents (pour plus de détails, on se référera à l'article correspondant). Chacune de ces transformations conduit à un modèle possible pour décrire la machine asynchrone. Dans la pratique, seuls certains modèles sont effectivement utilisés.

Le modèle à fuites secondaires avec l'ensemble ramené au stator est le plus fréquent dans la littérature car il comporte des éléments que l'on peut identifier relativement simplement et de manière suffisamment précise et il est simple d'emploi.

Avec :

· $\mathcal{N}_r = \mathcal{L}_S \cdot \left (\frac{\mathcal{L}_S \cdot \mathcal{L}_r}{\mathcal{M}_{rS}^2}-1 \right ) \,$

· $R_r^* = R_r \cdot \frac{\mathcal{L}_S^2}{\mathcal{M}_{rS}^2} \,$

Ces grandeurs ne sont pas calculables (en particulier R_r), mais l'important est de savoir que si l'on admet les hypothèses de départ, alors il existe un dipôle identique à celui représenté ci-dessus équivalent à une phase de la machine asynchrone alimentée par un système de tensions triphasées équilibré.

Il est intéressant pour les bilans de puissance de décomposer la résistance $\frac{R_r^*}{g} \,$ en deux termes :

· $R_r^* \,$ : résistance ramenée de l'enroulement rotorique, responsable des pertes par effet Joule au rotor (pertes Joule rotoriques).

· $R_r^* \cdot \frac{1-g}{g} \,$ : résistance fictive : la puissance qu'elle consomme correspond en réalité à la puissance utile de la phase considérée. (Puissance transformée en puissance mécanique par la machine).

Prise en compte des pertes fer[modifier]

On a considéré que le circuit magnétique était sans pertes, ce qui n'est pas le cas. Pour rendre compte des pertes fer qui dépendent du carré de l'alimentation, on ajoute dans ce modèle une résistance fictive R_F en parallèle avec l'inductance statorique.

Identifications des éléments du schéma équivalent[modifier]

Après avoir établi que le schéma précédent correspondait à une phase de la machine asynchrone, on peut identifier le modèle correspondant à une machine quelconque en réalisant trois essais :

Essai en continu[modifier]

Réalisé sur une phase de la machine, il permet de mesurer la résistance statorique R_S.

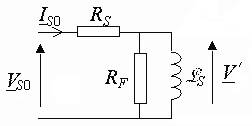
Essai au synchronisme : g = 0[modifier]

Lors d'un essai au synchronisme, le champ tournant et le rotor tournent à la même vitesse. Le glissement g est nul et 1/g tend vers l'infini. Le modèle équivalent d'une phase de la machine devient :

À l'aide d'un wattmètre, d'un ampèremètre et d'un voltmètre, on mesure la puissance active P₀, la puissance réactive $Q_0 = \sqrt{S_0^{2} - P_0^{2}}$ , le courant efficace I_S0 et la tension efficace V_S0

on obtient les trois équations :

· $P_0=R_sI_{S0}^2+\frac{V'^2}{R_F}$

· $Q_0=\frac{V'^2}{\mathcal{L}_S\omega}$

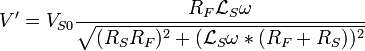
· $V'=V_{S0}\frac{R_F\mathcal{L}_S\omega}{\sqrt{(R_SR_F)^2+(\mathcal{L}_S\omega*(R_F+R_S))^2}}$

R_S étant connue, on peut calculer les trois inconnues : R_F, $\mathcal{L}_S \,$ et V'

Le courant I_S0 étant faible lors de l'essai au synchronisme, on peut généralement négliger la perte de tension due à la resistance statorique devant la tension V_S0. Les équations deviennent alors :

· $P_0=\frac{V_{S0}^2}{R_F}$

· $Q_0=\frac{V_{S0}^2}{\mathcal{L}_S\omega}$

On calcule alors directement R_F et $\mathcal{L}_S \,$ :

· $R_F=\frac{V_{S0}^2}{P_0}$

· $\mathcal{L}_S=\frac{V_{S0}^2}{Q_0\omega}$

Essai rotor bloqué et tension réduite : g = 1[modifier]

À vitesse nulle, le glissement g = 1. Cet essai est réalisé sous tension réduite afin de limiter l'intensité du courant à une valeur acceptable. Le modèle équivalent d'une phase de la machine devient :

À l'aide d'un wattmètre, d'un ampèremètre et d'un voltmètre, on mesure la puissance active P₁, la puissance réactive $Q_1 = \sqrt{S_1^{2} - P_1^{2}}$ , le courant efficace I_S1 et la tension efficace V_S1

· $P_1=R_S I_{S1}^2+V'^2 (\frac{1}{R_F}+\frac{R_r^*}{(\mathcal{N}_r \omega)^2+{R_r^*}^2})$

· $Q_1=V'^2 (\frac{1}{\mathcal{L}_S \omega}+\frac{\mathcal{N}_r \omega}{(\mathcal{N}_r \omega)^2+{R_r^*}^2})$

· $\underline V'= \underline V_{S1}- R_S \underline I_{S1} \Rightarrow V'= \ldots$

La tension V_S1 étant faible, les courants circulants dans R_F et $\mathcal{L}_S$ peuvent généralement être négligés devant I_S1. Les équations deviennent alors :

· $P_1=(R_S+R_r^*)I_{S1}^2$

· $Q_1=\mathcal{N}_r \omega I_{S1}^2$

L'identification des derniers paramètres de la machine est alors rapide :

· $R_r^*=\frac{P_1}{I_{S1}^2}-R_S$

· $\mathcal{N}_r = \frac{Q_1}{\omega I_{S1}^2}$

Caractéristiques électromécaniques[modifier]

Le schéma établi précédemment permet d'obtenir facilement les caractéristiques électromécaniques de la machine asynchrone monophasée :

En effet la puissance électromagnétique utile, c’est-à-dire celle transformée en énergie mécanique correspond pour chaque phase à la puissance consommée par la résistance $R_r^* \cdot \frac{1-g}{g} \,$

La puissance électromécanique totale pour les trois phases a donc pour expression :

$P_{em} =T_{em} \cdot \Omega = 3.R_r^* \cdot \frac{1-g}{g} \cdot I_r^2 \,$

Machine alimentée par un système de tensions de fréquence fixe[modifier]

Le modèle ci-dessus permet d'obtenir l'expression du couple soit en fonction du glissement, soit en fonction de la vitesse. Le calcul est très simplifié et peut être fait à la main si l'on néglige la résistance statorique. Dans ce cas, on ajoute une erreur de 2 ou 3 %, mais on obtient une courbe dont l'allure est proche de la réalité. De toute façon, on ne doit pas perdre de vue que ce ne sont que des modèles.

Dans le cadre de cette approximation on a :

$I_r^2 = \frac{V_S^2}{ (\mathcal{N}_r \omega_S)^2+(\frac{R_r^* }{g})^2} \,$

Avec $V_S \,$ : valeur efficace de la tension aux bornes d'une des phases du stator de la machine.

Couple électromagnétique en fonction du glissement[modifier]

De l'expression de la puissance et des deux équations ci-dessus on en déduit l'expression du couple électromagnétique en fonction du glissement g :

Pour une machine à p paires de pôles on a : $\Omega = (1-g) \cdot \frac{\omega_S}{p} \,$

Cela conduit à :

$T_{em}= 3 p \frac{V_S^2}{\omega_S} \cdot \frac{\frac{R_r^*}{g}}{ (\mathcal{N}_r \omega_S)^2+(\frac{R_r^* }{g})^2} \,$

$= 3 p \frac{V_S^2}{\omega_S} \cdot \frac{1}{(\frac{g (\mathcal{N}_r \omega_S)^2}{R_r^*})+ (\frac{R_r^* }{g})} \,$

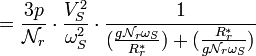
$= \frac{3 p}{\mathcal{N}_r} \cdot \frac{V_S^2}{ \omega_S^2} \cdot \frac{1}{(\frac{g \mathcal{N}_r \omega_S}{R_r^*})+ (\frac{R_r^* }{g \mathcal{N}_r \omega_S })} \,$

Le couple électromagnétique passe par un maximum $T_{max} = \frac{3 p}{2 \mathcal{N}_r} \cdot \frac{V_S^2}{ \omega_S^2} \,$ pour $g = g_{max} =\frac{R_r^*}{ \mathcal{N}_r \omega_S} \,$

En introduisant ce couple maximal et le glissement correspondant dans l'équation du couple électromagnétique on obtient la relation :

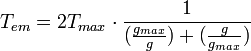
$T_{em}= 2 T_{max} \cdot \frac{1}{(\frac{g_{max}}{g})+ (\frac{g}{g_{max}})} \,$

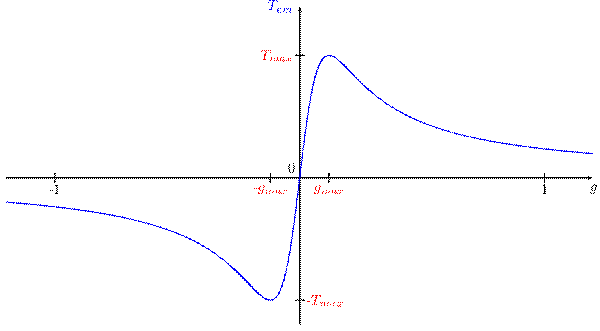
La courbe représentative de l'expression du couple en fonction du glissement possède une symétrie par rapport à l'origine :

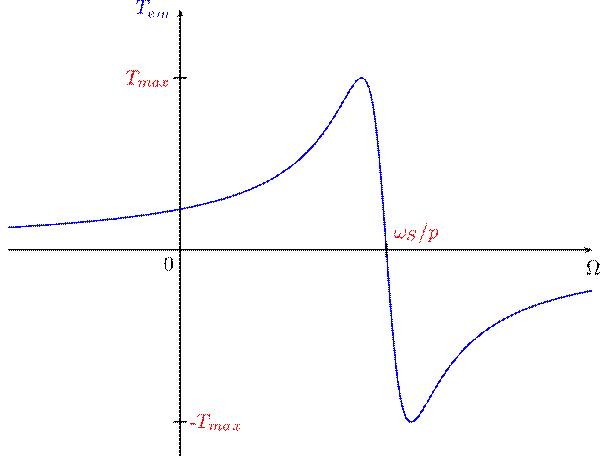
Couple électromagnétique en fonction de la vitesse de rotation[modifier]

Cette courbe est plus habituelle et plus concrète, elle se déduit simplement de la courbe en fonction du glissement grâce à la relation :

$\Omega = (1-g) \cdot \frac{\omega_S}{p} \,$

Les domaines de fonctionnement de la machine asynchrone[modifier]

Machine alimentée par un onduleur[modifier]

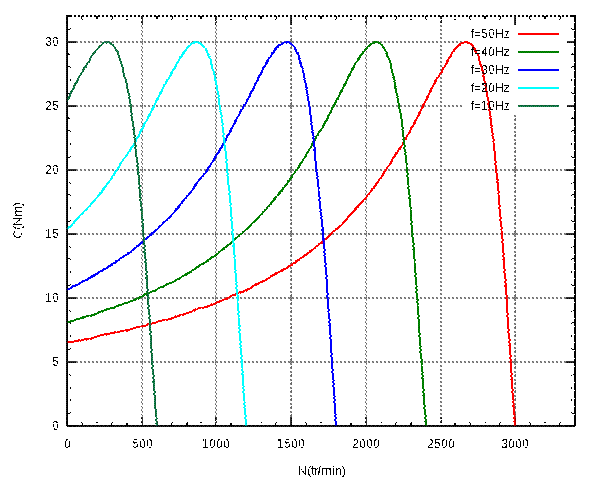
Réglage de la vitesse de rotation des moteurs asynchrones triphasés¹¹

Les onduleurs les plus répandus sont les onduleurs MLI (à modulation de largeur d'impulsion) dont le mode de commande permet de garder le rapport U₁/f constant et d'obtenir des courants quasiment sinusoïdaux. U₁ étant la valeur efficace du fondamental.

Commande en U/f[modifier]

Principe[modifier]

En régime sinusoïdal, la conservation du rapport U/f permet au circuit magnétique d'être dans le même état magnétique quelle que soit la fréquence d'alimentation. Autrement dit, la forme du cycle d'hystérésis parcouru par le circuit magnétique reste identique quelle que soit f. Ainsi, lorsque la fréquence diminue, la valeur efficace du fondamental de la tension diminuant dans les mêmes proportions, il n'y a pas de risque de saturation du matériau magnétique.

Ceci a pour conséquence qu'une commande qui maintient U₁/f constant, où U₁ représente la valeur efficace du fondamental, permet de conserver la même courbe de couple en fonction du glissement pour n'importe quelle fréquence d'alimentation. Les autres harmoniques présents, multiples de 5 et 7, créent des couples pulsants dont la moyenne est nulle.

Pour cela, la machine asynchrone est alimentée par un onduleur délivrant une tension de fréquence f et dont la valeur efficace du fondamental V₁ est telle que le rapport V₁/f est maintenu constant¹¹.

Mise en équation[modifier]

Lorsque le rapport U/f est constant on peut écrire pour la partie linéaire de la caractéristique couple-vitesse :

$T_{em} = Cte \cdot (n_S - n) \,$

[afficher]

Démonstration

La courbe du couple en fonction de n_S - n est unique.

Remarques[modifier]

Lors d'un démarrage (faible fem) à fort couple (courant important), la chute de tension due à la résistance statorique devient plus importante que la fem. Il est alors impossible d'obtenir le flux nominal dans la machine grâce à la loi U/f=cst. Pour compenser cela, les variateurs industriels proposent différentes lois U(f). Le choix de la loi à utiliser dépend de l'application.

Une fois que la tension nominale est atteinte, on augmente la fréquence d'alimentation du moteur sans augmenter sa tension. On parle alors de défluxage de la machine. Cela amène bien entendu une baisse du couple maximal délivrable par la machine. Un démarrage dans de telles conditions se fera donc à couple constant puis à puissance constante.

Inconvénients[modifier]

Les procédés de variation de vitesse pour les moteurs asynchrones sont générateurs de courants harmoniques.

Commande vectorielle[modifier]

Article détaillé : Commande vectorielle.

La commande vectorielle est un terme générique désignant l'ensemble des commandes tenant compte en temps réel des équations du système qu'elle commande. Le nom de ces commandes vient du fait que les relations finales sont vectorielles à la différence des commandes scalaires. Les relations ainsi obtenues sont bien plus complexes que celles des commandes scalaires, mais en contrepartie elles permettent d'obtenir de meilleures performances lors des régimes transitoires. Il existe des commandes vectorielles pour tous les moteurs à courant alternatif^11,19.

Bilans de puissance[modifier]

Bilan de puissance de la machine fonctionnant en moteur[modifier]

On utilise les notations suivantes :

· $P_a \,$ : puissance absorbée ou puissance électrique fournie à la machine

· $P_u \,$ : puissance utile ou puissance mécanique transmise à la charge

Les pertes sont généralement notées en minuscule :

· $p_{Js} \,$ : pertes par effet Joule dans le bobinage du stator

· $p_{fs} \,$ : pertes dans le fer du stator

· $p_{Jr} \,$ : pertes par effet Joule dans le cuivre (barres + anneaux) du rotor

· $p_{fr} \,$ : pertes dans le fer du rotor. Très souvent, on fait l’hypothèse qu’elles sont négligeables car ces dernières dépendent de la fréquence des courants qui induisent le champ magnétique dans le fer. Or la fréquence des courants dans le rotor ( $|g|f \,$ ), lors du fonctionnement normal de la machine alimentée en régime sinusoïdal de courant, est très faible. Néanmoins il faut parfois en tenir compte lorsque la machine est alimentée par un onduleur ou dans certains types de fonctionnement à fort glissement.

· $p_m \,$ : pertes mécaniques

Le schéma ci-dessous représente la transmission de la puissance à travers la machine :

$P_{tr} = P_a - p_{Js} - p_{fs} \,$ est la puissance transmise au rotor

On peut vérifier que $p_{Jr} = g . P_{tr} \,$ , d'où $P_u = (1 - g) P_{tr} - p_m \,$ si l'on néglige $p_{fr} \,$ .

Bilan de puissance de la machine fonctionnant en génératrice[modifier]

Par rapport au cas précédent, la puissance utile devient la puissance électrique fournie au réseau et la puissance mécanique est la puissance absorbée.

· $P_a \,$ : puissance absorbée = puissance mécanique fournie à la machine (en général, absorbée au niveau du rotor)

· $P_u \,$ : puissance utile = puissance électrique transmise au réseau (transmise par le stator).

Les pertes sont les mêmes que pour le fonctionnement en moteur.

Machine asynchrone monophasée[modifier]

La constitution interne d'une machine asynchrone monophasée est la même que celle d'une machine triphasée à la différence près, que son stator est composé d'un enroulement et non de trois. Le champ magnétique créé par une bobine monophasée est un champ pulsant et non tournant comme pour celui créé par trois bobines triphasées. Un champ pulsant peut se décomposer en deux champs tournants qui se déplacent dans des sens opposés. Chaque champ tournant tendant à entraîner la machine dans le même sens que lui. Lorsque le rotor est à l'arrêt, le couple créé par chacun des champs tournants est de même valeur. Ainsi, le moteur ne peut démarrer. Pour démarrer un tel moteur, il faut donc le lancer ou avoir recours à un dispositif annexe. Une fois le moteur lancé, et amené à sa vitesse nominale, le moteur possède un glissement proche de 0 pour l'un des champs tournants, et de 2 pour le second. Le couple créé par le premier champ étant plus important que le couple créé par celui de sens contraire, le moteur continue à tourner.

Les machines asynchrones monophasées ont des caractéristiques (couple/ puissance massique, rendement, facteur de puissance, etc.) plus faibles que leurs homologues multiphasées. Ces machines sont toujours utilisées en moteur et généralement limitées à des puissances de quelques kilowatts.

Dispositifs de démarrage[modifier]

Lorsqu'il est alimenté en monophasé, le moteur asynchrone nécessite un système de démarrage. Différentes solutions permettent une différenciation de ces moteurs :

· Les spires de Frager (ou bagues de déphasage) qui sont utilisées dans des dispositifs exigeant un couple assez faible au démarrage tels que les pompes de vidange demachines à laver, les ventilateurs électriques et d'autres petits appareils électroménagers. Voir : « Moteur à bague de démarrage ».

· Un enroulement auxiliaire de démarrage en série avec un condensateur, avec éventuellement un commutateur centrifuge de coupure : ce type de moteur peut généralement fournir un plus grand couple de démarrage. On les trouve dans les machines à laver et dans l'outillage électroportatif de puissance moyenne (supérieure à 1500 W).

· À l'arrêt le condensateur et l'enroulement de démarrage sont reliés à la source d'énergie, fournissant le couple de démarrage et déterminant le sens de rotation. Il suffit d'inverser l'enroulement auxiliaire pour que le moteur tourne dans l'autre sens.

· Usuellement, une fois le moteur lancé à une certaine vitesse, un interrupteur centrifuge ouvre le circuit de l'enroulement et du condensateur de démarrage.

Raccordement[modifier]

Le raccordement au réseau ou à un variateur de ces moteurs, monophasés et triphasés, passe par un bornier (plaque à borne) protégé par un boîtier fixé sur le moteur. L'accès au boîtier se fait généralement en démontant un couvercle étanche située sur le dessus. L'entrée du ou des câbles se fait par un (ou plusieurs) presse-étoupe chargé d'assurer l'étanchéité ainsi que le maintien mécanique du câble d'alimentation.

· Les six bornes des enroulements du stator des moteurs triphasés sont toujours placées de la même manière sur la plaque à bornes. Cette organisation particulière permet le raccordement soit en étoile, soit en triangle, suivant une procédure simple et standardisée.

Vue schématique d'une plaque à bornes. En noir, les enroulements.

Raccordement étoile

Raccordement en triangle.

Les moteurs triphasés sont susceptibles de tourner dans deux directions. Qu'ils soient connectés en étoile ou en triangle, l'inversion de leur sens de marche s'effectue simplement en permutant deux des conducteurs d'alimentation, par exemple U1 et V1 sur les schémas ci-dessus. Attention ! Une permutation circulaire des trois conducteurs n'inverse pas le sens de rotation.

Notes et références[modifier]

1. ↑ Guy Séguier et François Notelet, Électrotechnique industrielle.

2. ↑ Étude d’une éolienne basée sur une machine asynchrone [archive], Cndp.fr - Bases documentaires.

3. ↑ (en) Brevet U.S. 359748 [archive]

4. ↑ voir « Histoire de l'électricité »

5. ↑ (it) Museo Elettrico - Galileo Ferraris [archive], sur le site museoelettrico.com

6. ↑ association des entreprises électriques suisses [archive], sur le site strom.ch

7. ↑ Réseau ferré urbain [archive], sur le site metro-pole.net

8. ↑ Fiche technique du constructeur Alstom [archive] , sur le site alstom.com

9. ↑ Guide des solutions en automatisme 2007 de Schneider Electric § 3-1,§ 3-4 et § 3-6. [archive], sur le site automation.schneider-electric.com

10. ↑ Patrick Abati, « Modulation de largeur d'impulsion [archive] » sur sitelec.org, janvier 2003 [PDF].

11. ↑ ^a,^b,^c^et^d Patrick Abati, « Réglage de la vitesse de rotation des moteurs asynchrones triphasés [archive] » sur sitelec.org, origine : académie d'Aix-Marseille, 23 février 2002.

12. ↑ Trois fois le courant nominal de la machine, selon Mikhail Kostenko et Ludvik Piotrovski, Machines électriques – Machines à courant alternatif, tome II, Éditions de Moscou (Mir), 1969, (3^e édition 1979), p. 558.

13. ↑ Cinq à huit fois le courant nominal, selon « Démarrage et freinage des moteurs asynchrones triphasés » [archive], sur le site sitelec.org (origine de l'académie d'Aix-Marseille), consulté le 3 mai 2010.

14. ↑ ^a,^b,^c,^d,^e,^f,^g,^h,^i,^j^et^k Patrick Abati, « Démarrage et freinage des moteurs asynchrones triphasés [archive] » sur sitelec.org, origine : académie d'Aix-Marseille, 23 février 2002.

15. ↑ M. A. Iliovici, Cours moyen d'électricité industrielle, vol. 2 : génératrice et moteurs a courant alternatifs ; transformateurs ; applications industrielles de l'électricité, Paris, Librairie de l'Enseignement Technique Léon Eyrolles, 1945, 496 p., « Démarrage d'un moteur d'induction polyphasé », p. 78.

quatorzième édition

16. ↑ Tom Bishop, Squirrel cage rotor testing, EASA convention, June 2003 (disponible online sur le site de Pumping Machinery [archive]

17. ↑ [PDF] Centre de mutualisation et de recherche pédagogique en technologie et sciences industrielles de l'académie de Poitiers [archive]

18. ↑ André Bonnet, « Machine asynchrone triphasée [archive] » sur sitelec.org, origine : académie d'Aix-Marseille, 9 avril 2002.

19. ↑ Introduction à la commande vectorielle des machines asynchrones [archive] sur geea.org.