|
Peter
Gwozdz |
Results: |
#NOME? |
SBP
= Statistical Background Percent |
11 |
End
of the Gap |
|
|
|
|
|
|
|
|
|
|
15,0% |
|
0,0 |
minimum
from this column |
|
|
|
|
|
|
Poisson
Confidence Interval (Demonstration) |
|
| Input
data in column A |
|
#NOME? |
Statistical Mountain
Number |
|
11 |
Mountain Number |
|
Poisson tail |
|
#NOME? |
minimum from this column |
|
| 70% |
Confidence (70% is
recommended) |
#NOME? |
Statistical (Mountain)
Background |
|
0 |
Gap Number |
|
10 |
Cutoff integer check of
user input |
|
for use in the Poisson
function |
|
#NOME? |
minimum SBP value from
this column |
|
1 |
Number of samples; must be an integer |
| 10 |
Cutoff |
|
10 |
Cutoff |
|
0,0 |
Type Outliers |
|
2 |
Gap check |
|
|
|
|
|
|
70% |
Enter the confidence |
|
| 2 |
Gap |
|
2 |
Gap |
|
|
|
0,0 |
(Mountain) Background |
4 |
Gap display check |
|
|
|
|
| 4 |
Gap frequency display |
|
|
|
= Average Gap Frequency |
|
|
|
|
|
Statistical |
|
|
#NOME? |
Calculated Low Confidence
Limit |
|
|
To reduce the x-axis on the graph |
|
#NOME? |
Statistical Gap Number |
|
SBP Trials |
|
End = End of Gap = Cutoff
+ Gap -1 |
|
Gap |
Gap |
|
#NOME? |
Calculated High
Confidence Limit |
|
|
Delete cells at the bottom;
all 5 of these columns |
|
#NOME? |
Statistical Average Gap
Frequency |
|
Cutoff |
Gap |
Cutoff |
Gap |
End |
Mountain |
M+G |
Gap |
|
Statistical Numbers |
Average |
Average |
SBP |
|
|
Do not delete the rows, just highlight the data & press
Delete |
|
|
= Statistical Background |
|
|
|
|
|
|
Number |
|
Number |
Mountain |
Gap |
Frequency |
Frequency |
|
|
|
I downloaded the Poisson
functions from: |
|
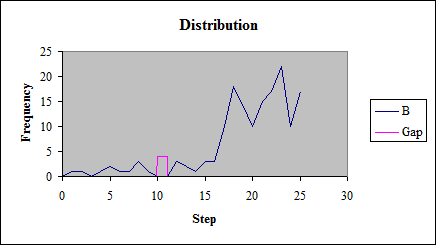
| B |
< Label |
|
Step |
Total |
Frequency |
Gap |
Display |
|
11,0 |
Size (of the Type) |
|
|
|
10 |
2 |
11 |
11 |
11 |
0 |
#NOME? |
##### |
0,0 |
#NOME? |
#NOME? |
This is the requested
Cutoff & Gap |
|
http://statpages.org/confint.html |
|
| 1 |
< Copy of the
"Total" |
0 |
0 |
0 |
0 |
0 |
|
#NOME? |
Size confidence minimum |
|
9 |
1 |
9 |
1 |
9 |
10 |
11 |
1 |
#NOME? |
##### |
1,0 |
#NOME? |
#NOME? |
These blue rows are the
"neighbor" values |
|
These Poisson functions
are Macros |
|
| 2 |
Column A |
1 |
1 |
1 |
1 |
0 |
|
#NOME? |
Size confidence maximum |
|
9 |
2 |
9 |
2 |
10 |
10 |
11 |
1 |
#NOME? |
##### |
0,5 |
#NOME? |
#NOME? |
|
Cutoff / Gap with +/- One |
|
So Excel gives a warning
when opening this file |
| 4 |
Start at row 11 |
2 |
2 |
1 |
|
0 |
|
|
9 |
3 |
9 |
3 |
11 |
10 |
11 |
1 |
#NOME? |
##### |
0,3 |
#NOME? |
#NOME? |
|
There may be duplicates
in here |
|
Peter Gwozdz |
|
| 5 |
|
3 |
2 |
0 |
3 |
0 |
|
|
10 |
1 |
10 |
1 |
10 |
11 |
11 |
0 |
#NOME? |
##### |
0,0 |
#NOME? |
#NOME? |
|
See if your values are
"local minimums" |
|
|
|
| 5 |
|
4 |
3 |
1 |
4 |
0 |
|
|
10 |
3 |
10 |
3 |
12 |
11 |
14 |
3 |
#NOME? |
##### |
1,0 |
#NOME? |
#NOME? |
|
|
|
|
| 6 |
|
5 |
5 |
2 |
5 |
0 |
|
|
11 |
1 |
11 |
1 |
11 |
11 |
11 |
0 |
#NOME? |
##### |
0,0 |
#NOME? |
#NOME? |
|
|
|
|
| 7 |
|
6 |
6 |
1 |
6 |
0 |
|
|
11 |
2 |
11 |
2 |
12 |
11 |
14 |
3 |
#NOME? |
##### |
1,5 |
#NOME? |
#NOME? |
|
|
|
|
|
| 8 |
|
7 |
7 |
1 |
7 |
0 |
|
|
11 |
3 |
11 |
3 |
13 |
11 |
16 |
5 |
#NOME? |
##### |
1,7 |
#NOME? |
#NOME? |
|
|
|
|
| 8 |
|
8 |
10 |
3 |
8 |
0 |
|
|
8 |
0 |
8 |
1 |
8 |
7 |
10 |
3 |
#NOME? |
##### |
3,0 |
#NOME? |
#NOME? |
The rest of these are 2
counts beyond your values |
|
|
|
| 8 |
|
9 |
11 |
1 |
9,9 |
0 |
|
|
8 |
1 |
8 |
1 |
8 |
7 |
10 |
3 |
#NOME? |
##### |
3,0 |
#NOME? |
#NOME? |
|
There may be "false
minimums" at another gap beyond your gap |
|
|
| 9 |
|
10 |
11 |
0 |
10 |
4 |
|
|
8 |
2 |
8 |
2 |
9 |
7 |
11 |
4 |
#NOME? |
##### |
2,0 |
#NOME? |
#NOME? |
|
And duplicates |
|
|
|
| 12 |
|
11 |
11 |
0 |
11 |
4 |
|
|
8 |
3 |
8 |
3 |
10 |
7 |
11 |
4 |
#NOME? |
##### |
1,3 |
#NOME? |
#NOME? |
|
|
|
|
| 12 |
|
12 |
14 |
3 |
11,1 |
0 |
|
|
8 |
4 |
8 |
4 |
11 |
7 |
11 |
4 |
#NOME? |
##### |
1,0 |
#NOME? |
#NOME? |
|
|
|
|
| 12 |
|
13 |
16 |
2 |
13 |
0 |
|
|
9 |
0 |
9 |
1 |
9 |
10 |
11 |
1 |
#NOME? |
##### |
1,0 |
#NOME? |
#NOME? |
|
|
|
|
| 13 |
|
14 |
17 |
1 |
14 |
0 |
|
|
9 |
4 |
9 |
4 |
12 |
10 |
14 |
4 |
#NOME? |
##### |
1,0 |
#NOME? |
#NOME? |
|
|
| 13 |
|
15 |
20 |
3 |
15 |
0 |
|
|
10 |
0 |
10 |
1 |
10 |
11 |
11 |
0 |
#NOME? |
##### |
0,0 |
#NOME? |
#NOME? |
|
|
| 14 |
|
16 |
23 |
3 |
16 |
0 |
|
|
10 |
4 |
10 |
4 |
13 |
11 |
16 |
5 |
#NOME? |
##### |
1,3 |
#NOME? |
#NOME? |
|
|
| 15 |
|
17 |
33 |
10 |
17 |
0 |
|
|
11 |
0 |
11 |
1 |
11 |
11 |
11 |
0 |
#NOME? |
##### |
0,0 |
#NOME? |
#NOME? |
|
|
|
|
| 15 |
|
18 |
51 |
18 |
18 |
0 |
|
|
11 |
4 |
11 |
4 |
14 |
11 |
17 |
6 |
#NOME? |
##### |
1,5 |
#NOME? |
#NOME? |
|
|
| 15 |
|
19 |
65 |
14 |
19 |
0 |
|
|
12 |
0 |
12 |
1 |
12 |
11 |
14 |
3 |
#NOME? |
##### |
3,0 |
#NOME? |
#NOME? |
|
|
| 16 |
|
20 |
75 |
10 |
20 |
0 |
|
|
12 |
1 |
12 |
1 |
12 |
11 |
14 |
3 |
#NOME? |
##### |
3,0 |
#NOME? |
#NOME? |
|
| 16 |
|
21 |
90 |
15 |
21 |
0 |
|
12 |
2 |
12 |
2 |
13 |
11 |
16 |
5 |
#NOME? |
##### |
2,5 |
#NOME? |
#NOME? |
|
|
| 16 |
|
22 |
107 |
17 |
22 |
0 |
|
12 |
3 |
12 |
3 |
14 |
11 |
17 |
6 |
#NOME? |
##### |
2,0 |
#NOME? |
#NOME? |
|
|
| 17 |
|
23 |
129 |
22 |
23 |
0 |
|
12 |
4 |
12 |
4 |
15 |
11 |
20 |
9 |
#NOME? |
##### |
2,3 |
#NOME? |
#NOME? |
|
|
| 17 |
|
24 |
139 |
10 |
24 |
0 |
|
|
| 17 |
|
25 |
156 |
17 |
25 |
0 |
|
|
| 17 |
|
|
|
| 17 |
|
|
|
| 17 |
|
|
|
| 17 |
|
|
|
| 17 |
|
|
|
| 17 |
|
|
|
| 17 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 18 |
|
|
|
| 19 |
|
|
|
| 19 |
|
|
|
| 19 |
|
|
|
| 19 |
|
|
|
| 19 |
|
| 19 |
|
| 19 |
|
| 19 |
|
| 19 |
|
| 19 |
|
| 19 |
|
| 19 |
|
| 19 |
|
| 19 |
|
| 20 |
|
| 20 |
|
| 20 |
|
| 20 |
|
| 20 |
|
| 20 |
|
| 20 |
|
| 20 |
|
| 20 |
|
| 20 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 21 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 22 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 23 |
|
| 24 |
|
| 24 |
|
| 24 |
|
| 24 |
|
| 24 |
|
| 24 |
|
| 24 |
|
| 24 |
|
| 24 |
|
| 24 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 25 |
|
| 26 |
|
| 26 |
|
| 26 |
|
| 26 |
|
| 26 |
|
| 26 |
|
| 26 |
|
| 26 |
|
| 26 |
|
| 27 |
|
| 27 |
|
| 27 |
|
| 27 |
|
| 27 |
|
| 27 |
|
| 27 |
|
| 27 |
|
| 27 |
|
| 28 |
|
| 28 |
|
| 28 |
|
| 29 |
|
| 29 |
|
| 29 |
|
| 29 |
|
| 29 |
|
| 29 |
|
| 29 |
|
| 30 |
|
| 30 |
|
| 30 |
|
| 30 |
|
| 30 |
|
| 30 |
|
| 30 |
|
| 32 |
|
| 34 |
|
| 68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

