|
"La
chance n'est qu'un mot pour désigner la ténacité dans les projets"
EMERSON
|
SOMMAIRE
:
|
|
|
|
INTRODUCTION
|
|
I -
|
LES FAITS
|
|
|
- point de vue du distributeur d'énergie
- point de vue du client
|
|
II -
|
LE COS Phi
: UN PEU DE THEORIE :
|
|
|
- qui est-il ???
- une expérience...
|
|
III -
|
QUELQUES
VALEURS DE COS Phi :
|
|
IV -
|
INCONVENIENTS
D'UN MAUVAIS COS Phi :
|
|
V -
|
COMMENT
AMELIORER LE COS Phi :
|
|
VI -
|
OU
INSTALLER UNE BATTERIE DE CONDENSATEUR :
|
|
|
|
INTRODUCTION :
Tout système électrique utilisant le
courant alternatif met en jeu deux formes d'énergie : l'énergie
active et l'énergie réactive. Dans les processus industriels
utilisant l'énergie électrique seule l'énergie active est transformée au sein
de l'outil de production en énergie mécanique, thermique, lumineuse, etc...
L'autre, l'énergie réactive sert notamment à l'alimentation des circuits
magnétiques des machines électriques (moteurs, autotransformateurs, etc...).
Par ailleurs, certains constituants des réseaux électriques de transport et
de distribution (transformateurs, lignes, etc...) consomment également dans
certains cas d'exploitation de l'énergie réactive.
I - LES FAITS :
- Point de vue du distributeur
d'énergie :
La circulation des puissances active et
réactive provoque des pertes actives et des chutes de tension dans les
conducteurs. Les pertes actives réduisent le rendement global des réseaux et
les chutes de tension sont néfastes au maintien d'une bonne tension que doit
le distributeur à ses clients. Ainsi est-il donc préférable sur le plan
technique de les produire le plus près possible des lieux de consommation.
- Pour la puissance active, on montre qu'il est
plus économique de la produire d'une manière centralisée et de la
distribuer ensuite aux clients. Le coût du transport est bien moins
élevé que le surcoût d'une production réalisée localement.
- En revanche, pour la puissance réactive, il
est économiquement plus intéressant de la produire, en tout ou partie,
localement par des générateurs d'énergie réactive autonomes comme les
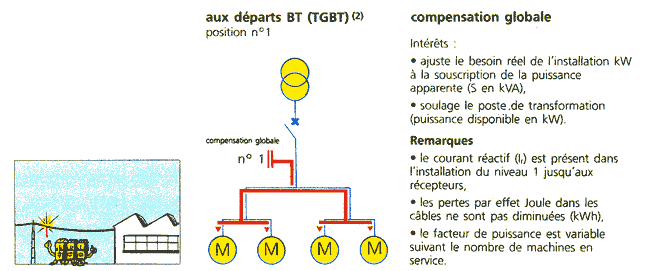
condensateurs par exemple. Cette pratique est appelée COMPENSATION.
- Point de vue du client :
Comme pour le distributeur, le
transport de la puissance réactive sur le réseau intérieur du client entraîne
les inconvénients suivants :
- surcharge ou surdimensionnement
des installations (transfo, câbles, etc...)
- pertes actives plus importantes
dans ces ouvrages
- augmentation de la facture EDF.
|
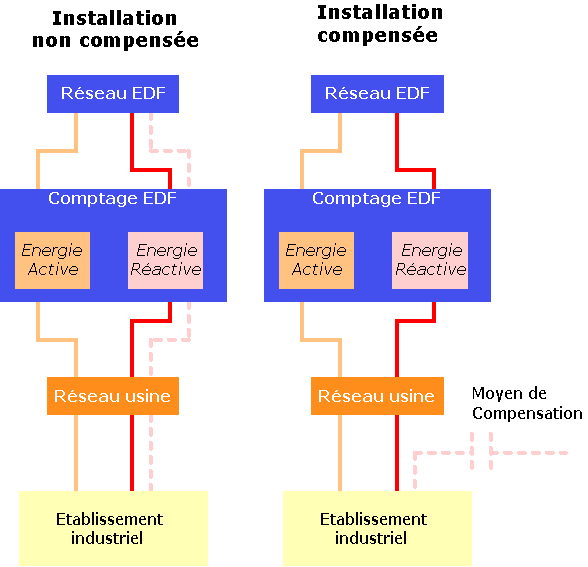
Cheminement
des puissances ACTIVE et REACTIVE
|
|
|
II - LE COS Phi : UN PEU
DE THEORIE :
- Qui est-il :
Nous venons de voir que tous les moteurs et
tous les appareils fonctionnant en courant alternatif et comprenant un
circuit magnétique absorbent deux formes d'énergie :
- une énergie dite active, qui se manifeste par
un travail sur l'arbre d'un moteur par exemple.
- une énergie dite réactive, qui ne sert qu'à
aimanter le fer du circuit magnétique.
A chacune de ces énergies correspond un courant
actif (Ia), en phase avec la tension du réseau et un courant
réactif (Ir), appelé aussi courant magnétisant. Celui-ci étant déphasé
de 90° en arrière par rapport au courant actif. Les deux courants actif et
réactif se composent vectoriellement pour former le courant
apparent, déphasé d'un angle Phi par rapport au courant actif. Ce
courant dit apparent est cependant bien réel, puisque c'est celui qui
parcourt les divers conducteurs du circuit, depuis la source jusqu'au
récepteur inclus, et qui provoque entre autre l'échauffement de ces
conducteurs, donc les pertes d'énergie par effet joule.
|
Représentation des courants par FRESNEL :
|
|

|
D'après la
représentation ci contre et sachant qu'en monophasé :
- P = U.It.Cos Phi
- Q = U.It.Sin Phi
- S = U.It
Rappel :
- Sin Phi = Opp/Hyp
- Cos Phi = Adj/Hyp
- Tg Phi = Opp/Adj
- Ia = It.Cos Phi
donc It = Ia/Cos Phi
- Ir = It.Sin Phi donc It =
Ir/Sin Phi
Nous pouvons donc écrire :
- P = U.Ia
- Q = U.Ir
- S = U.It
|
De cela nous pouvons donc voir qu'il est
très simple de retranscrire le diagramme des courants donné précedemment par
le diagramme suivant :
|
Du
facteur de puissance à la puissance réactive...
|
|

|
Remarque :
Les équations ci contre donneraient les
mêmes résultats si nous étions en triphasé.
LE FACTEUR DE PUISSANCE
EST LA PROPORTION DE PUISSANCE ACTIVE DANS LA PUISSANCE APPARENTE.
Nous pourrons donc dire,
et puisque le facteur de puissance est égal au rapport de la puissance
active par la puissance apparente que :
- le facteur de puissance est égal
au Cosinus Phi.
- le Cosinus Phi = P/S ou Ia/It
- P < S donc 0 < Cosinus Phi
< 1.
- It sera d'autant plus grand que
le Cosinus Phi sera petit...
|
- Une expérience mettant en
évidence l'incidence d'une variation de Cos Phi :
Considérons deux appareils électriques fréquemment
employés, fonctionnant en monophasé sous la tension de 220V alternatif :
- Un four électrique à résistances
- Un moteur monophasé dont le rendement sera
égal à 1.
|
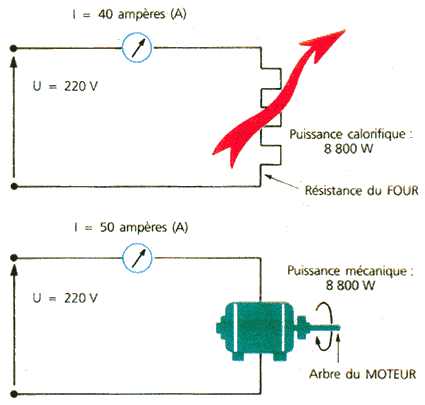
Une
expérience... :-))
|
|
|
A puissance utile égale
nous pouvons voir que :
- I moteur > I résistances
- Smoteur > Srésistances
Ainsi pour une puissance active
identique (P=8800W), le moteur appelle sur le réseau une puissance apparente
(S = U.I = 220.50 = 11000VA) supérieure
à celle qui est appelée par le four (S = U.I =
220.40 = 8800VA). Cela est dû au fait que pour disposer de 8800W de
puissance active (moteur), il faut aimanter le circuit magnétique de ce dernier
et donc consommer de l'énergie REACTIVE.
Calculons le Cosinus Phi dans chaque cas
:
- résistances : Cos Phi = P/S =
8800/8800 = 1
- moteur : Cos Phi = P/S =
8800/11000 = 0,8
|
III - QUELQUESVALEURS DE COS
Phi :
|
APPAREIL
|
Cos
Phi
|
Tg Phi
|
OBSERVATIONS
|
|
Moteurs asynchrones
ordinaires chargés à :
|
|
|
|
|
|
Lampes à incandescence
|
1
|
0
|
|
|
Lampes à fluorescence
|
0,5
|
1,73
|
Ces lampes sont
généralement compensées. Le FP est alors satisfaisant.
|
|
Lampes à fluorescence
compensées
|
0,93
|
0,39
|
|
|
Fours à résistances
|
1
|
0
|
Sauf si le réglage est
assuré par gradateur à thyristors
|
|
Fours à induction
|
0,85
|
0,62
|
Cette valeur suppose une
compensation par condensateurs prévue par le constructeur.
|
|
Machines à souder à
résistances
|
0,8
à 0,9
|
0,75
à 0,48
|
|
|
Postes statiques
monophasés de soudage à l'arc
|
0,5
|
1,73
|
Sauf si la compensation
à été prévue par le constructeur.
|
|
Chaudières à
thermoplongeurs
|
1
|
0
|
Sauf si la régulation
est assurée par des thyristors fonctionnant à angle de phase; les thyristors
à trains d'onde ne modifiant pas le facteur de puissance.
|
|
|
|
|
|
IV - INCONVENIENTS D'UN
MAUVAIS COS Phi :
Comme nous venons de le voir précedement,
pour une même puissance utile fournie par un appareil électrique, il faut transporter
dans tous les circuits électriques une intensité d'autant plus grande que le
Cos Phi est faible, cela entraîne :
- Une augmentation du montant de la facture
EDF.(une consommation excessive d'énergie réactive peut également
entraîner une majoration sous forme de pénalité du montant de votre
facture EDF : difficulté qu'a EDF à prévoir la quantité d'énergie à
produire).
- Une surcharge ou un surdimensionnement de
l'installation. En effet, si le Cos Phi diminue, It (courant réellement
transporté) augmente, or, les facteurs qui limitent la puissance
maximale que peut transmettre une ligne sont, d'une part la chute de
tension (fonction de I), d'autre part la température maximale admissible
par l'isolant : à peu près 70° pour du PVC (fonction de I²)
Ce qu'il faut retenir :
Un mauvais Cosinus Phi :
- accroît les chutes de tension dans les câbles,
- augmente les pertes par effet joule lors du
transport de l'énergie électrique
- entraîne une surfacturation EDF par une
surconsommation ou une pénalité
- dégrade la capacité de transport de l'énergie
électrique par des câbles
- entraîne un surdimensionnement des
installations neuves : câbles (section), transfo (S), etc...
- entraîne des renforcements prématurés des
installations existantes
- Ne laisse pas de réserve de marche au secondaire
du transformateur
V - COMMENT AMELIORER LE COS
Phi :
L'amélioration du Cosinus Phi doit passer
par l'installation d'un moyen de compensation qui constitue la solution la
plus efficace : très généralement une ou plusieurs batteries de condensateurs
(Véritable générateur d'énergie réactive : I en avance de 90° sur U réseau)
Rappel : Q = P.Tg (Phi)
Soit un appareil ou groupe d'appareils
appelant une puissance active P (en Kw) et une puissance réactive (en KVAR).
On souhaite réduire la Tg(Phi) à une valeur plus faible Tg(Phi').
|
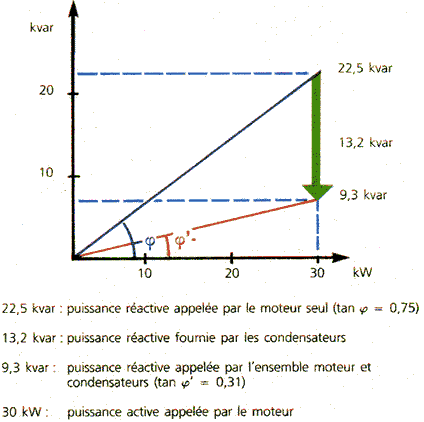
Puissance
réactive des condensateurs à installer :
|
|
|
Q = P.Tg(Phi) et Q' = P.Tg(Phi')
La puissance du ou des condensateurs à installer sera égale à : Qb =
P(Tg(Phi) - Tg(Phi')) = Q - Q'
Dans l'exemple précité : Qb = 30(0,75-0,31) = 13,2 KVAR
NOTA : la
valeur du Cos Phi ou Tg Phi évoluant avec le temps il convient d'utiliser
les valeurs moyennes de ces derniers pour l'utilisation de la formule
précédente "Qb = P (Tg(Phi)-Tg(Phi'))"
|
Calcul de la capacité
des condensateurs à installer :
La quantité d'énergie réactive
fournie par un condensateur est Qc = U².C.w
avec :
- U = tension aux bornes du
condensateur
- C = capacité du condensateur
- w = 2.PI.f = pulsation du réseau
d'alimentation
Si nous avons un couplage
triangle alors 3 condensateurs :
=> Quantité d'énergie
réactive à apporter par condensateur : Qb / 3 d'où Qc = Qb / 3 ce qui nous
donne :
C = (Pabs(Tg(Phi)-Tg(Phi'))/(3.U².w)
Si nous prenons les valeurs de
l'exemple précédent et que le réseau d'alimentation est de 3 x 400V~ alors C
= 87,6 MicroFarad. Si nous avions couplé nos condensateur en étoile, nous
aurions obtenus une capacité par condensateur de C = 264,9 MicroFarad sous
une tension d'alimentation de 230V~.
Conclusion :
- La capacité des condensateurs
couplés en triangle est trois fois plus petite.
- La tension à supporter par les
condensateurs lors du couplage étoile est dans un rapport de racine de
3.
- les dimensions de la batterie de
condensateurs couplés en triangle seront plus petites.
VI - OU INSTALLER UNE
BATTERIE DE CONDENSATEUR :
|